题目内容
17. 如图,要围成一个矩形花圃.花圃的一边利用足够长的墙,另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.
如图,要围成一个矩形花圃.花圃的一边利用足够长的墙,另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.(l)能围成面积为96平方米的矩形花圃吗?如果能,说明围的方法;如果不能,说明理由;
(2)如何围,花圃的面积最大?最大面积是多少?
分析 (1)设AB边的长为x米,则BC=32-2x,然后利用矩形的面积公式列出方程解答即可;
(2)求得矩形ABCD面积的二次函数解析式,利用二次函数的性质求最大值即可.
解答 解:(1)设AB=xm,则BC=(32-2x)m
由题意得:x(32-2x)=96
解得:x1=12,x2=4
当x1=12时,32-2x=8;
当x2=4时,32-2x=24;
答:AB=12m,BC=8m或AB=4m,BC=24米是可以围成.
(2)设:花圈的面积为s,AB=x,
s=x(32-2x),
s=-2x2+32x,
当x=-$\frac{32}{2×(-2)}$=8时,
s有最大值=-2×82+32×8=128,
∴当所围矩形花圈的AB=8m时,有最大面积128m2.
点评 此题主要考查的是二次函数的应用,一元二次方程的应用,掌握二次函数的性质、矩形的面积计算方法是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
7.有一组数据如下:3,a,4,6,7,若它们的平均数是5,则这组数据的方差是( )
| A. | 10 | B. | $\sqrt{10}$ | C. | $\sqrt{2}$ | D. | 2 |
2.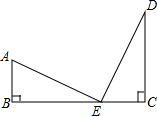 如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
 如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )| A. | 仅① | B. | 仅①③ | C. | 仅①③④ | D. | 仅①②③④ |
9.若-$\frac{{5a}^{3}{b}^{n+2}}{2}$是一个5次单项式,则n的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |

 如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:
如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答: 如图,AB∥CD,直线EF分别交AB、CD于点E、F,且∠1=47°15′,则∠2=132°45′.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,且∠1=47°15′,则∠2=132°45′.