题目内容
 已知:如图,在矩形OABC中,边OA、OC分别在x、y轴上,且A(10,0),C(0,6).点D在BC边上,AD=AO.
已知:如图,在矩形OABC中,边OA、OC分别在x、y轴上,且A(10,0),C(0,6).点D在BC边上,AD=AO.(1)试说明OD平分∠CDA;
(2)求点D的坐标.
考点:矩形的性质,坐标与图形性质
专题:
分析:(1)由矩形的性质可知:BC∥AO,所以∠CDO=∠DOA,再有条件AD=AO可得∠ADO=∠AOD,所以∠CDO=∠ADO,即OD平分∠CDA;
(2)过D作DE⊥AO,DE的长为D的纵坐标,求出OE的长则为D的横坐标.
(2)过D作DE⊥AO,DE的长为D的纵坐标,求出OE的长则为D的横坐标.
解答: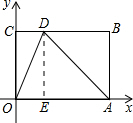 (1)证明:
(1)证明:
∵四边形OABC是矩形,
∴BC∥AO,
∴∠CDO=∠DOA,
∵AD=AO,
∴∠ADO=∠AOD,
∴∠CDO=∠ADO,
即OD平分∠CDA;
(2)过D作DE⊥AO,
则四边形OCDE是矩形,
∴DE=OC=6,
∴D的纵坐标为6,
∵AD=AO=10,
∴AE=
=8,
∴OE=AO-AE=2,
∴D的横坐标为2,
∴D的坐标为(2,6).
 (1)证明:
(1)证明:∵四边形OABC是矩形,
∴BC∥AO,
∴∠CDO=∠DOA,
∵AD=AO,
∴∠ADO=∠AOD,
∴∠CDO=∠ADO,
即OD平分∠CDA;
(2)过D作DE⊥AO,
则四边形OCDE是矩形,
∴DE=OC=6,
∴D的纵坐标为6,
∵AD=AO=10,
∴AE=
| AD2-DE2 |
∴OE=AO-AE=2,
∴D的横坐标为2,
∴D的坐标为(2,6).
点评:本题考查了矩形的性质以及判定、等腰三角形的性质和判定以及勾股定理的运用,题目的综合性较强,但难度不大.

练习册系列答案
相关题目
如果|a|=a,则( )
| A、a是正数 |
| B、a是负数 |
| C、a是零 |
| D、a 是正数或零 |
 如图,已知AC⊥CB,DB⊥CB,AB⊥DE,AB=DE,E是BC的中点.
如图,已知AC⊥CB,DB⊥CB,AB⊥DE,AB=DE,E是BC的中点. 如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.  如图,已知矩形纸片ABCD,AB=1.5,AD=1,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AD、AB交于点F、G(F≠D).
如图,已知矩形纸片ABCD,AB=1.5,AD=1,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AD、AB交于点F、G(F≠D). 已知一次函数y=kx+b的图象平行于直线y=-2x+4,且经过点A(2,-2).
已知一次函数y=kx+b的图象平行于直线y=-2x+4,且经过点A(2,-2). 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边上的动点,连接DE,OE.
如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边上的动点,连接DE,OE. 如图,点A′、B′、C′、D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′,求证:A′C′与B′D′互相垂直且相等.
如图,点A′、B′、C′、D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′,求证:A′C′与B′D′互相垂直且相等.