题目内容
2.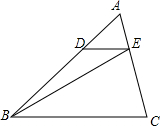 已知:如图,DE∥BC,S△ADE=3,S△EBC=18,则S△BDE为( )
已知:如图,DE∥BC,S△ADE=3,S△EBC=18,则S△BDE为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 设S△BDE=x,由$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{AD}{BD}$、$\frac{{S}_{△ABE}}{{S}_{△BCE}}$=$\frac{AE}{CE}$,结合$\frac{AD}{DB}$=$\frac{AE}{CE}$得出$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{{S}_{△ABE}}{{S}_{△BCE}}$,再将x的值代入即可得出答案.
解答 解:设S△BDE=x.
∵$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{AD}{BD}$,$\frac{{S}_{△ABE}}{{S}_{△BCE}}$=$\frac{AE}{CE}$,
∵DE∥BC,
∴$\frac{AD}{DB}$=$\frac{AE}{CE}$,
∵S△ADE=3,S△BCE=18,
∴$\frac{{S}_{△ADE}}{{S}_{△BDE}}$=$\frac{{S}_{△ABE}}{{S}_{△BCE}}$,
∴$\frac{3}{x}$=$\frac{3+x}{18}$,
解得:x1=-9(舍),x2=6.
∴S△BDE=6;
故选:C.
点评 本题考查了平行线分线段成比例定理,三角形的面积,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
17. 如图,在△ABC中,中线AD、CE相交于点G,AG=6,则AD的长为( )
如图,在△ABC中,中线AD、CE相交于点G,AG=6,则AD的长为( )
 如图,在△ABC中,中线AD、CE相交于点G,AG=6,则AD的长为( )
如图,在△ABC中,中线AD、CE相交于点G,AG=6,则AD的长为( )| A. | 18 | B. | 9 | C. | 8 | D. | 3 |
7.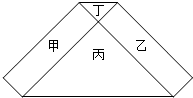 如图,六边形是由甲、乙两个矩形和丙、丁两个等腰三角形所组成的,其中甲、乙的面积的和等于丙、丁的面积的和.若丙的腰长为2,且丁的面积比丙的小,则丁的腰长为( )
如图,六边形是由甲、乙两个矩形和丙、丁两个等腰三角形所组成的,其中甲、乙的面积的和等于丙、丁的面积的和.若丙的腰长为2,且丁的面积比丙的小,则丁的腰长为( )
 如图,六边形是由甲、乙两个矩形和丙、丁两个等腰三角形所组成的,其中甲、乙的面积的和等于丙、丁的面积的和.若丙的腰长为2,且丁的面积比丙的小,则丁的腰长为( )
如图,六边形是由甲、乙两个矩形和丙、丁两个等腰三角形所组成的,其中甲、乙的面积的和等于丙、丁的面积的和.若丙的腰长为2,且丁的面积比丙的小,则丁的腰长为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
 如图:从A地到B地走路线①最近,此判断的根据是两点之间线段最短.
如图:从A地到B地走路线①最近,此判断的根据是两点之间线段最短.