题目内容
7.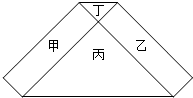 如图,六边形是由甲、乙两个矩形和丙、丁两个等腰三角形所组成的,其中甲、乙的面积的和等于丙、丁的面积的和.若丙的腰长为2,且丁的面积比丙的小,则丁的腰长为( )
如图,六边形是由甲、乙两个矩形和丙、丁两个等腰三角形所组成的,其中甲、乙的面积的和等于丙、丁的面积的和.若丙的腰长为2,且丁的面积比丙的小,则丁的腰长为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
分析 设出丁的腰长为a,根据矩形的性质判断出丙和丁是等腰直角三角形,再用面积建立方程即可.
解答 解:设丁的腰长为a,且a<2,
∵甲、乙是两个矩形,
∴丙和丁的顶角和为180°,且互为对顶角,
∴丙和丁是等腰直角三角形,
∵甲面积+乙面积=丙面积+丁面积,
∴2a+2a=$\frac{1}{2}$×22+$\frac{1}{2}$×a2,
∴4a=2+$\frac{1}{2}$a2,
∴a2-8a+4=0,
∴a=$\frac{8±4\sqrt{3}}{2}$=4$±2\sqrt{3}$,
∵4+2$\sqrt{3}$>2,不合题意舍,
4-2$\sqrt{3}$<2,合题意,
∴a=4-2$\sqrt{3}$,
故选:D.
点评 本题主要考查了等腰三角形的性质和矩形的性质及一元二次方程的应用,解本题的关键是列出一元二次方程.

练习册系列答案
相关题目
17.下列分数中不能化为有限小数的是( )
| A. | $\frac{7}{25}$ | B. | $\frac{7}{32}$ | C. | $\frac{3}{80}$ | D. | $\frac{5}{12}$ |
15. 小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
 小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )| A. | 50人中必有2人的生日相同 | B. | 100人中必有2人的生日相同 | ||
| C. | 365人中必有2人的生日相同 | D. | 367人中必有2人的生日相同 |
2.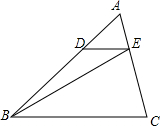 已知:如图,DE∥BC,S△ADE=3,S△EBC=18,则S△BDE为( )
已知:如图,DE∥BC,S△ADE=3,S△EBC=18,则S△BDE为( )
 已知:如图,DE∥BC,S△ADE=3,S△EBC=18,则S△BDE为( )
已知:如图,DE∥BC,S△ADE=3,S△EBC=18,则S△BDE为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
19. 校服裙子的展开图可近似看做是( )
校服裙子的展开图可近似看做是( )
 校服裙子的展开图可近似看做是( )
校服裙子的展开图可近似看做是( )| A. |  | B. |  | C. |  | D. |  |
16.如图,根据根据图中提供的信息,可知一个杯子的价格是( )


| A. | 51元 | B. | 35元 | C. | 8元 | D. | 7.5元 |