题目内容
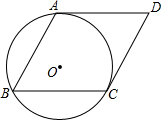 如图,⊙O经过菱形ABCD的三个顶点A、B、C,若∠B=60°,试判断直线AD与⊙O的位置关系,并说明理由.
如图,⊙O经过菱形ABCD的三个顶点A、B、C,若∠B=60°,试判断直线AD与⊙O的位置关系,并说明理由.考点:切线的判定,菱形的性质
专题:
分析:根据菱形的性质得出AB=AD=DC=BC,∠B=∠D=60°,求出△ABC和△ADC是等边三角形,求出∠OAC=30°,∠DAC=60°,求出∠DAO=90°,根据切线的判定得出即可.
解答: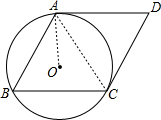 解:直线AD与⊙O的位置关系是相切,
解:直线AD与⊙O的位置关系是相切,
理由是:∵四边形ABCD是菱形,
∴AB=AD=DC=BC,∠B=∠D=60°,
∴△ABC和△ADC是等边三角形,
∴∠DAC=60°,
∵⊙O过A、B、C,
∴⊙O是等边△ABC的外接圆,
∴∠OAC=30°,
∴∠OAD=90°,
∴AD是⊙O的切线.
 解:直线AD与⊙O的位置关系是相切,
解:直线AD与⊙O的位置关系是相切,理由是:∵四边形ABCD是菱形,
∴AB=AD=DC=BC,∠B=∠D=60°,
∴△ABC和△ADC是等边三角形,
∴∠DAC=60°,
∵⊙O过A、B、C,
∴⊙O是等边△ABC的外接圆,
∴∠OAC=30°,
∴∠OAD=90°,
∴AD是⊙O的切线.
点评:本题考查了菱形的性质,等边三角形的性质,切线的判定的应用,解此题的关键是求出∠DAO=90°,题目比较好,难度适中.

练习册系列答案
相关题目
若一次函数y=kx+b,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值( )
| A、减小2 | B、增加2 |
| C、减小4 | D、增加4 |
若x≠0,则
+
=( )
| |x| |
| x |
| x |
| |x| |
| A、-1或1 | B、0 |
| C、1 | D、-2或2 |
下列说法正确的是( )
| A、正比例函数是一次函数 |
| B、不是正比例函数就不是一次函数 |
| C、正比例函数不是一次函数 |
| D、一次函数是正比例函数 |
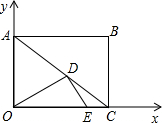 如图,在矩形ABCD中,AO=3,OC=4,以O为坐标原点,OC为x轴,OA为y轴建立平面直角坐标系.设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为t秒.
如图,在矩形ABCD中,AO=3,OC=4,以O为坐标原点,OC为x轴,OA为y轴建立平面直角坐标系.设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为t秒. 如图,在8×8网格中,每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.
如图,在8×8网格中,每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.