题目内容
 如图,在8×8网格中,每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.
如图,在8×8网格中,每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.(1)画出以C为旋转中心,将△ABC顺时针旋转90°后得到的△A′B′C;
(2)求点B旋转到点B′的路线长;(结果保留π)
(3)在旋转过程中,直接写出线段AB扫过的面积.(结果保留π)
考点:作图-旋转变换,弧长的计算,扇形面积的计算
专题:
分析:(1)根据图形旋转的性质画出将△ABC顺时针旋转90°后得到的△A′B′C即可;
(2)先根据勾股定理求出BC的长,再根据扇形的面积公式即可得出结论;
(3)根据线段AB扫过的面积=S扇形BCB′-S扇形ACA′即可得出结论.
(2)先根据勾股定理求出BC的长,再根据扇形的面积公式即可得出结论;
(3)根据线段AB扫过的面积=S扇形BCB′-S扇形ACA′即可得出结论.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)∵BC=
=
,
∴S扇形BCB′=
=
π;
(3)∵AC=
=
,
∴线段AB扫过的面积=S扇形BCB′-S扇形ACA′=
π-
=
π-
π=
π.
 解:(1)如图所示;
解:(1)如图所示;(2)∵BC=
| 12+32 |
| 10 |
∴S扇形BCB′=
90π×(
| ||
| 360 |
| 5 |
| 2 |
(3)∵AC=
| 12+22 |
| 5 |
∴线段AB扫过的面积=S扇形BCB′-S扇形ACA′=
| 5 |
| 2 |
90π×(
| ||
| 360 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
点评:本题考查的是作图-旋转变换,熟知图形旋转的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示的标志中,不是轴对称图形的有( )
A、 |
B、 |
C、 |
D、 |
若方程(a-2)x|a|-3x=1是关于x的一元二次方程,则a是( )
| A、2 | B、-2 | C、±2 | D、±1 |
下列各式y=2x、y=
、y=|x|-1、|y|=x、y=x2中y是x的函数的个数( )
| 1 |
| x |
| A、5 | B、4 | C、3 | D、2 |
 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧 |
| AMB |
| A、30° | B、45° |
| C、60° | D、不能确定 |
若am•a3=a5,则m的值为( )
| A、1 | B、2 | C、3 | D、4 |
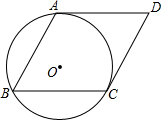 如图,⊙O经过菱形ABCD的三个顶点A、B、C,若∠B=60°,试判断直线AD与⊙O的位置关系,并说明理由.
如图,⊙O经过菱形ABCD的三个顶点A、B、C,若∠B=60°,试判断直线AD与⊙O的位置关系,并说明理由. 已知:右图是二次函数y=(x-m)2+k的图象,其顶点坐标为M(1,-4).
已知:右图是二次函数y=(x-m)2+k的图象,其顶点坐标为M(1,-4).