题目内容
19.解方程:(1)(2x+3)2-25=0
(2)2x2-4x=-1(用公式法解)
(3)(2x-3)2-5(2x-3)+6=0
(4)x2+2x-1=0(用配方法解)
分析 (1)利用因式分解法解方程;
(2)先把方程化为一般式,然后利用求根公式法解方程;
(3)把方程看作关于2x-3的一元二次方程,然后利用因式分解法解方程;
(4)利用配方法解方程.
解答 解:(1)(2x+3+5)(2x+3-5)=0,
所以x1=-4,x2=1;
(2)2x2-4x+1=0,
△=(-4)2-4×2×1=8,
x=$\frac{4±\sqrt{8}}{2×2}$=$\frac{2±\sqrt{2}}{2}$,
所以x1=$\frac{2+\sqrt{2}}{2}$,x2=$\frac{2-\sqrt{2}}{2}$;
(3)(2x-3-2)(2x-3-3)=0,
所以x1=$\frac{5}{2}$,x2=3;
(4)x2+2x=1,
x2+2x+1=2,
(x+1)2=2,
x+1=±$\sqrt{2}$,
所以x1=-1+$\sqrt{2}$,x2=-1-$\sqrt{2}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )
如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )
 如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )
如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )| A. | 1.5cm | B. | 2cm | C. | 3cm | D. | 4cm |
8.某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是( )
| A. | 289(1-2x)=256 | B. | 256(1+x)2=289 | ||
| C. | 289(1-x)2=256 | D. | 289-289(1-x)-289(1-x)2=256 |
9.下列运用等式的性质,变形不正确的是( )
| A. | 若x=y,则x-5=y-5 | B. | 若a=b,则ac=bc | C. | 若x=y,则x+a=y+a | D. | 若x=y,则$\frac{x}{a}$=$\frac{y}{a}$ |
 A、B两城相距600千米,甲、乙两车从A城出发驶向B城,乙车的速度为75千米/时,甲车先走100千米乙车才出发,甲车到达B卸完货后立即返回A城,如图它们离A城的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.
A、B两城相距600千米,甲、乙两车从A城出发驶向B城,乙车的速度为75千米/时,甲车先走100千米乙车才出发,甲车到达B卸完货后立即返回A城,如图它们离A城的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.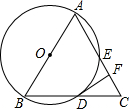 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作⊙O的切线,交AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作⊙O的切线,交AC于F.