题目内容
12.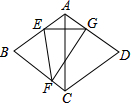 如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6$\sqrt{2}$,则FG的长为3$\sqrt{6}$.
如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6$\sqrt{2}$,则FG的长为3$\sqrt{6}$.
分析 首先证明△ABC,△ADC都是等边三角形,再证明FG是菱形的高,根据2•S△ABC=BC•FG即可解决问题.
解答 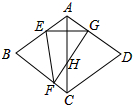 解:∵四边形ABCD是菱形,∠BAD=120°,
解:∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD是等边三角形,
∵EG⊥AC,
∴∠AEG=∠AGE=30°,
∵∠B=∠EGF=60°,
∴∠AGF=90°,
∴FG⊥BC,
∴2•S△ABC=BC•FG,
∴2×$\frac{\sqrt{3}}{4}$×(6$\sqrt{2}$)2=6$\sqrt{2}$•FG,
∴FG=3$\sqrt{6}$.
故答案为3$\sqrt{6}$.
点评 本题考查菱形的性质、等边三角形的判定和性质、翻折变换、菱形的面积等知识,记住菱形的面积=底×高=对角线乘积的一半,属于中考常考题型.

练习册系列答案
相关题目
2.从1,2,3,6中任意选两个数,记作a和b,那么点(a,b)在函数y=$\frac{6}{x}$图象上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
20.(-$\frac{1}{2}$)-2的倒数是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
7. 某住宅小区五月份1日至5如每天用水量变化情况如图所示,那么这5天平均每天用水量的中位数是( )
某住宅小区五月份1日至5如每天用水量变化情况如图所示,那么这5天平均每天用水量的中位数是( )
 某住宅小区五月份1日至5如每天用水量变化情况如图所示,那么这5天平均每天用水量的中位数是( )
某住宅小区五月份1日至5如每天用水量变化情况如图所示,那么这5天平均每天用水量的中位数是( )| A. | 28 | B. | 32 | C. | 34 | D. | 36 |
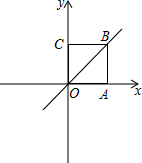 如图,点B(2,n)是直线y=k1x(k1≠0)上的点,如果直线y=k1x(k1≠0)平分∠yOx,BA⊥x轴于A,BC⊥y轴于C.
如图,点B(2,n)是直线y=k1x(k1≠0)上的点,如果直线y=k1x(k1≠0)平分∠yOx,BA⊥x轴于A,BC⊥y轴于C.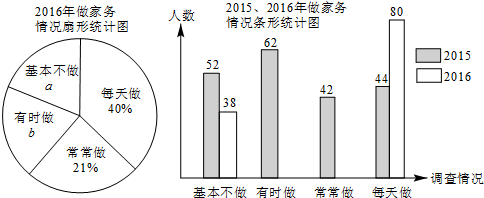
 如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.
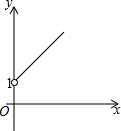
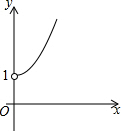
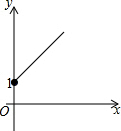
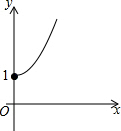
如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )