题目内容
2.从1,2,3,6中任意选两个数,记作a和b,那么点(a,b)在函数y=$\frac{6}{x}$图象上的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 先画树状图展示所有、12种等可能的结果数,然后根据反比例函数图象上点的坐标特征找出点(a,b)在函数y=$\frac{6}{x}$图象上的结果数,再利用概率公式求解.
解答 解:画树状图为: 、
、
共有12种等可能的结果数,其中点(a,b)在函数y=$\frac{6}{x}$图象上的结果数为4,
所以点(a,b)在函数y=$\frac{6}{x}$图象上的概率=$\frac{4}{12}$=$\frac{1}{3}$.
故选B.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了反比例函数图象上点的坐标特征.

练习册系列答案
相关题目
13.下列命题正确的是( )
| A. | 若分式$\frac{{{x^2}-4}}{2x-4}$的值为零,则x值为±2 | |
| B. | 若ab>0,则a>0、b>0 | |
| C. | 平行四边形对角互补 | |
| D. | 三个角相等的三角形是等边三角形 |
10. 已知直线a∥b,∠1和∠2互余,∠3=121°,那么∠4等于( )
已知直线a∥b,∠1和∠2互余,∠3=121°,那么∠4等于( )
 已知直线a∥b,∠1和∠2互余,∠3=121°,那么∠4等于( )
已知直线a∥b,∠1和∠2互余,∠3=121°,那么∠4等于( )| A. | 159° | B. | 149° | C. | 139° | D. | 21° |
17.在-$\sqrt{2}$,0,-2,1,-1这五个数中,最大的数和最小的是的和是( )
| A. | 0 | B. | -$\sqrt{2}$ | C. | -2 | D. | -1 |
7.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{(-3)^{2}}$ |
14.已知$\sqrt{a-2}$+(b+3)2=0,则(a+b)2016的值为( )
| A. | 0 | B. | 2016 | C. | -1 | D. | 1 |
11.下列计算中正确的是( )
| A. | 2x3-x3=2 | B. | x3•x2=x6 | C. | x2+x3=x5 | D. | x3÷x=x2 |
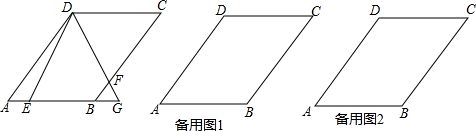
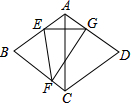 如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6$\sqrt{2}$,则FG的长为3$\sqrt{6}$.
如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6$\sqrt{2}$,则FG的长为3$\sqrt{6}$.