题目内容
3.已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点.求抛物线的解析式.分析 把点A(-1,0)、B(3,0)分别代入二次函数y=x2+bx+c得到关于b与c的方程组,然后解方程组求出b、c即可.
解答 解:把点A(-1,0)、B(3,0)分别代入y=x2+bx+c得,
$\left\{\begin{array}{l}{0=1-b+c}\\{0=9+3b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
∴抛物线解析式为y=x2-2x-3.
点评 本题考查了利用待定系数法求二次函数的解析式,设二次函数的解析式为y=ax2+bx+c(a≠0),然后把图象上三个点的坐标分别代入得到关于a、b、c的方程组,解方程组求出a、b、c的值,从而确定二次函数的解析式是解答此题的关键.

练习册系列答案
相关题目
14.一个多边形的每个外角是60°,则该多边形边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
11.已知$\frac{a}{b}$=$\frac{1}{2}$,则$\frac{a+b}{b}$的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{3}{2}$ |
8.t2-(t+1)(t-5)的计算结果正确的是( )
| A. | -4t-5 | B. | 4t+5 | C. | t2-4t+5 | D. | t2+4t-5 |
 如图,在⊙O中,半径OC⊥AB于点D,连结BC.
如图,在⊙O中,半径OC⊥AB于点D,连结BC.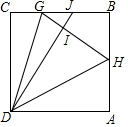 正方形ABCD中,∠GDH=45°,DI⊥GH并延长交BC于点J,GJ=5,GH=I0,求DJ长.
正方形ABCD中,∠GDH=45°,DI⊥GH并延长交BC于点J,GJ=5,GH=I0,求DJ长.