题目内容
16.直角三角形的外接圆和内切圆半径分别是5和2,则该直角三角形中较小的锐角的正弦值是$\frac{3}{5}$.分析 利用直角三角形的斜边为直径,内切圆半径为两直角边的和与斜边的差的一半,若设直角三角形的斜边为c,两直角边分别为a、b,则c=2×5=10,$\frac{a+b-c}{2}$=2,加上勾股定理可计算出a、b的值,然后根据正弦的定义求解.
解答 解:设直角三角形的斜边为c,两直角边分别为a、b,
根据题意得c=2×5=10,$\frac{a+b-c}{2}$=2,
∴c=10,a+b=14,
而a2+b2=c2,
∴(14-b)2+b2=100,解得b=8或b=6,
当b=8时,a=6;当b=6时,a=8,
∴三角形的两直角边为6、8,
∴该直角三角形中较小的锐角的正弦值=$\frac{6}{10}$=$\frac{3}{5}$.
故答案为$\frac{3}{5}$.
点评 本题考查了三角形内心的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了三角形的外心.

练习册系列答案
相关题目
6.下列各组式子中,两个单项式是同类项的是( )
| A. | 2a与a2 | B. | xy2与x2y | C. | 5a2b与a2b | D. | 0.3mn2与0.3my2 |
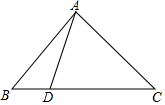 在△ABC中,∠A=90°,AB=AC,D为BC边上一点,求证:BD2+CD2=2AD2.
在△ABC中,∠A=90°,AB=AC,D为BC边上一点,求证:BD2+CD2=2AD2.