题目内容
1．先化简，再求值：（1+$\frac{2}{x-2}$）÷$\frac{{x}^{2}-x}{{x}^{2}-4}$（其中x是整数，且-3＜x＜3）．分析 首先把括号内的分式通分相加，把除法转化为乘法，然后进行约分即可化简，再根据x的范围确定x的值，代入求解即可．
解答 解：原式=$\frac{x-2+2}{x-2}$•$\frac{（x+2）（x-2）}{x（x-1）}$=$\frac{x}{x-2}$•$\frac{（x+2）（x-2）}{x（x-1）}$=$\frac{x+2}{x-1}$．
∵x是整数，且-3＜x＜3，
x≠0，±2，1．
∴x=-1．
则当x=-1时，原式=$\frac{1}{-2}$=-$\frac{1}{2}$．
点评 本题考查了分式的化简求值，正确利用分式有意义的条件，确定x的取值是关键．
练习册系列答案
相关题目
如图，直线y=kx+b与x轴、y轴分别相交于点A、B，与抛物线y=x2相交于C，D，AC=$\sqrt{5}$，且sin∠OAB=$\frac{\sqrt{5}}{5}$，求该直线的解析式及点D的坐标．
如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作EF⊥AB于点F，交AC的延长线于点E．
如图，抛物线y=-x2+bx+c与x轴交于点M，N，与y轴交于点A（0，1），且经过点B（1，1），过点B作BC⊥x轴，交x轴于点C．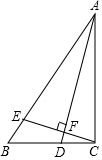
如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点D为边BC上一动点（不与点B、C重合），联结AD，过点C作CF⊥AD，分别交AB、AD于点E、F，设DC=x，$\frac{AE}{BE}$=y．
如图，平面直角坐标系中，已知点A（a-b，2$\sqrt{3}$），B（a+b，0），AB=4，且$\sqrt{a-3b}$+（a+b-4）2=0，C为x轴上点B右侧的动点，以AC为腰作等腰△ACD，使AD=AC，∠CAD=∠OAB，直线DB交y轴于点P．