题目内容
18.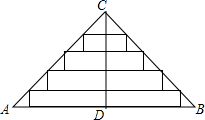 如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40厘米,若将斜边上的高CD进行五等分,然后裁出4张宽度相等的长方形纸条,则这4张纸条的长度之和是80$\sqrt{2}$厘米.
如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40厘米,若将斜边上的高CD进行五等分,然后裁出4张宽度相等的长方形纸条,则这4张纸条的长度之和是80$\sqrt{2}$厘米.
分析 首先利用勾股定理可求出AB的长,再根据斜边上的高CD进行五等分,可得EF和AB的比值,可求出EF的长,以此类推即可求出GH,IJ,KL的长度,问题得解.
解答 解:∵△ABC是等腰直角三角形,AC=BC=40cm,如下图所示:
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=40$\sqrt{2}$cm,
∵斜边上的高CD进行五等分,
∴$\frac{EF}{AB}$=$\frac{1}{5}$ ,
,
又∵AB=40$\sqrt{2}$cm,
∴EF=8$\sqrt{2}$cm,
同理,GH=16$\sqrt{2}$cm,
IJ=24$\sqrt{2}$cm,
KL=32$\sqrt{2}$cm,
∴这4张纸条的长度之和是:8$\sqrt{2}$+16$\sqrt{2}$+24$\sqrt{2}$+32$\sqrt{2}$=80$\sqrt{2}$cm,
故答案为:80$\sqrt{2}$.
点评 此题考查了相似三角形的应用以及勾股定理的运用,此题难度适中,注意掌握数形结合思想的应用,解题的关键是利用相似三角形的性质:对应高之比等于相似比得到EF和AB的比值.

练习册系列答案
相关题目
9.长方形的周长为60cm,其中一条边为x(其中x>0),面积为ycm2,则在这个长方形中,y与x的关系可以写为( )
| A. | y=60x-2x2 | B. | y=30x-x2 | C. | y=$\frac{1}{2}$x2-60 | D. | y=$\frac{1}{2}$x2-30 |
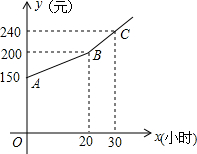 为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.
为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示. 如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.
如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.