题目内容
9.已知关于x的一元二次方程x2+2x+k-1=0有实数根,k为正整数.(1)求k的值;
(2)当此方程有两个非零的整数根时,求关于x的二次函数y=x2+2x+k-1的图象的对称轴和顶点坐标.
分析 (1)根据一元二次方程x2+2x+k-1=0有实数根,可推△≥0,求出k的取值范围,得出k的数值即可;
(2)分别把k的值代入方程2x2+4x+k-1=0,解得结果根据方程有两个非零的整数根进行分析,确定k的值,进一步利用二次函数的性质确定对称轴和顶点坐标.
解答 解:(1)∵关于x的一元二次方程x2+2x+k-1=0有实数根,
∴△=4-4(k-1)≥0.
∴k≤2.
∵k为正整数,
∴k=1,2;
(2)设方程x2+2x+k-1=0的两根为x1,x2,则
x1+x2=-2,x1•x2=k-1,
当k=1时,方程x2+2x+k-1=0有一个根为零;
当k=2时,方程x2+2x+k-1=0有两个相同的非零实数根-1.
k=2符合题意.
二次函数y=x2+2x+1=(x+1)2,
对称轴是x=-1,顶点坐标是(-1,0).
点评 此题考查一元二次方程根的判别式,二次函数图象与性质,利用根的判别式确定k的数值是解决问题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 下面的哪个平面图形绕轴旋转一周得到的几何体从上面看到的如图所示( )
下面的哪个平面图形绕轴旋转一周得到的几何体从上面看到的如图所示( )



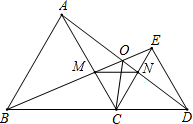 如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连OC、MN,则下列结论①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC;⑤若∠ADE=20°,则∠BED=100°;⑥OB=AO+OC,其中正确的结论个数有( )
如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连OC、MN,则下列结论①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC;⑤若∠ADE=20°,则∠BED=100°;⑥OB=AO+OC,其中正确的结论个数有( ) 已知:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AC方向匀速运动,速度为2cm/s.当点Q停止运动时,点P也停止运动.连接PQ、PD、QD.设运动时间为t(s)(0<t<4).
已知:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AC方向匀速运动,速度为2cm/s.当点Q停止运动时,点P也停止运动.连接PQ、PD、QD.设运动时间为t(s)(0<t<4).
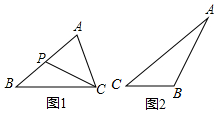 王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB.
王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB.