Question

【题目】某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如下两个不完整的统计图（校服型号以身高作为标准，共分为6种型号）．

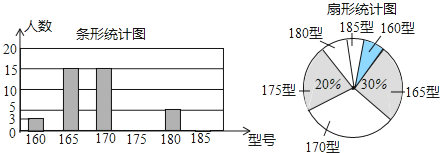
根据以上信息，解答下列问题：

（Ⅰ）该班共有 名学生，其中穿175型校服的学生有 名；

（Ⅱ）在条形统计图中，请把空缺部分补充完整．

（Ⅲ）在扇形统计图中，185型校服所对应的扇形圆心角的大小为 ；

（Ⅳ）该班学生所穿校服型号的众数为 ，中位数为 ．

（Ⅴ）如果该校预计招收新生600名，根据样本数据，估计新生中穿170型校服的学生大约有 名．

Answer 1

【答案】（Ⅰ）50，10；（Ⅱ）补图见解析；（Ⅲ）14．4°；（Ⅳ）165和170，170；（Ⅴ）180．

【解析】

试题（Ⅰ）根据穿165型的人数与所占的百分比列式进行计算即可求出学生总人数，再乘以175型所占的百分比计算即可得解；

（Ⅱ）先求出185型的人数，然后补全统计图；

（Ⅲ）用185型所占的百分比乘以360°计算即可得解；

（Ⅳ）根据众数的定义以及中位数的定义解答；

（Ⅴ）用招收新生600名乘以新生中穿170型校服的学生所占的百分比，即可求出答案．

试题解析：（Ⅰ）根据题意得：

15÷30%=50（名），

50×20%=10（名），

答：该班共有50名学生，其中穿175型校服的学生有10名；

（Ⅱ）185型的学生人数为：50-3-15-15-10-5=50-48=2（名），

补全统计图如图所示：

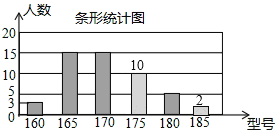
（Ⅲ）185型校服所对应的扇形圆心角为：×360°=14．4°；

（Ⅳ）165型和170型出现的次数最多，都是15次，则众数是165和170；

共有50个数据，第25、26个数据都是170，则中位数是170．

（Ⅴ）根据题意得：600×=180（名），

答：新生中穿170型校服的学生大约有180名．