题目内容
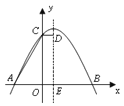
【题目】已知抛物线![]() 经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线
经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线![]() :
:![]() (a≠0),
(a≠0),
(1)试求抛物线![]() 的函数解析式;
的函数解析式;
(2)求证: 抛物线 ![]() 与x轴一定有两个不同的交点;
与x轴一定有两个不同的交点;
(3)若a=1
①抛物线![]() 、
、![]() 顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线
顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线![]() 、
、![]() 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;
②已知直线MN分别与x轴、![]() 、
、![]() 分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
【答案】(1)![]() (2)证明见解析(3)8
(2)证明见解析(3)8
【解析】试题分析:
试题解析:
(1)设![]() 的解析式为y=a(x-1)(x-5),
的解析式为y=a(x-1)(x-5),
当x=0,y=-5,
∴-5=a(-1)×(-5),∴a=-1,
∴![]() =
=![]() 。
。
(2)△=![]() =
=![]() =
=![]() =
=![]() >0,
>0,
∴抛物线![]() 与x轴一定有两个不同的交点。
与x轴一定有两个不同的交点。
(3)当a=1时,①![]() 、
、![]() 的顶点分别为(3,4)、(2,-1),当2≤x≤3时,抛物线
的顶点分别为(3,4)、(2,-1),当2≤x≤3时,抛物线![]() 、
、![]() 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;
② ![]() 的顶点为(2,-1),对称轴为x=2,与x轴的交点为(3,0),(1,0),
的顶点为(2,-1),对称轴为x=2,与x轴的交点为(3,0),(1,0),![]() 与
与![]() 的交点为(1,0),(4,3),
的交点为(1,0),(4,3),
当1≤m≤4时,
MN=![]() =
=![]() =
=![]() =-2
=-2![]() +
+![]() 。
。
当x=![]() 时,MN最大
时,MN最大![]() ;
;
当4<m≤5时,MN=![]() =
=![]() ,
,
∵MN=![]() 有最小值,但在对称轴右边MN随x增大而增大,
有最小值,但在对称轴右边MN随x增大而增大,
当m=5时,MN最大=2![]() 25-50+8=8。
25-50+8=8。
综合上述MN最大值为8

练习册系列答案
相关题目