ÌâÄ¿ÄÚÈÝ
 ÈçÍŒ£¬ÔÚµÈÑüRt¡÷ABCÖУ¬¡ÏC=90¡ã£¬AC=8£¬FÊÇAB±ßÉϵÄÖе㣬µãD¡¢E·Ö±ðÔÚAC¡¢BC±ßÉÏÔ˶¯£¬ÇÒ±£³ÖAD=CE£®Á¬œÓDE¡¢DF¡¢EF£®ÔÚŽËÔ˶¯±ä»¯¹ý³ÌÖУ¬ÏÂÁÐœáÂÛ£º
ÈçÍŒ£¬ÔÚµÈÑüRt¡÷ABCÖУ¬¡ÏC=90¡ã£¬AC=8£¬FÊÇAB±ßÉϵÄÖе㣬µãD¡¢E·Ö±ðÔÚAC¡¢BC±ßÉÏÔ˶¯£¬ÇÒ±£³ÖAD=CE£®Á¬œÓDE¡¢DF¡¢EF£®ÔÚŽËÔ˶¯±ä»¯¹ý³ÌÖУ¬ÏÂÁÐœáÂÛ£º¢Ù¡÷DFEÊǵÈÑüÖ±œÇÈýœÇÐΣ»¢ÚËıßÐÎCDFE²»¿ÉÄÜΪÕý·œÐΣ»¢Û¡÷CDEÓë¡÷DAF²»¿ÉÄÜÈ«µÈ£»¢ÜËıßÐÎCDFEµÄÃæ»ý±£³Ö²»±ä£»¢Ý¡÷CDEÃæ»ýµÄ×îŽóֵΪ8£®
ÆäÖÐÕýÈ·µÄœáÂÛÊÇ£š¡¡¡¡£©
| A¡¢¢Ù¢Ú¢Û | B¡¢¢Ù¢Û¢Ü |
| C¡¢¢Û¢Ü¢Ý | D¡¢¢Ù¢Ü¢Ý |
¿Œµã£ºÈ«µÈÈýœÇÐεÄÅжšÓëÐÔÖÊ,µÈÑüÖ±œÇÈýœÇÐÎ
ךÌ⣺ŒÆËãÌâ
·ÖÎö£º×÷³£¹æžšÖúÏßÁ¬œÓCF£¬ÓÉSAS¶šÀí¿ÉÖ€¡÷CFEºÍ¡÷ADFÈ«µÈ£¬ŽÓ¶ø¿ÉÖ€¡ÏDFE=90¡ã£¬DF=EF£®ËùÒÔ¡÷DEFÊǵÈÑüÖ±œÇÈýœÇÐΣ»ÓÉžî²¹·š¿ÉÖªËıßÐÎCDFEµÄÃæ»ý±£³Ö²»±ä£»
¡÷DEFÊǵÈÑüÖ±œÇÈýœÇÐÎDE=
DF£¬µ±DFÓëBCŽ¹Ö±£¬ŒŽDF×îСʱ£¬DEÈ¡×îСֵ4
£¬¡÷CDE×îŽóµÄÃæ»ýµÈÓÚËıßÐÎCDEFµÄÃæ»ýŒõÈ¥¡÷DEFµÄ×îСÃæ»ý£®
¡÷DEFÊǵÈÑüÖ±œÇÈýœÇÐÎDE=
| 2 |
| 2 |
œâŽð£º œâ£ºÁ¬œÓCF£»
œâ£ºÁ¬œÓCF£»
¡ß¡÷ABCÊǵÈÑüÖ±œÇÈýœÇÐΣ¬
¡à¡ÏFCB=¡ÏA=45¡ã£¬CF=AF=FB£»
¡ßAD=CE£¬
¡à¡÷ADF¡Õ¡÷CEF£»
¡àEF=DF£¬¡ÏCFE=¡ÏAFD£»
¡ß¡ÏAFD+¡ÏCFD=90¡ã£¬
¡à¡ÏCFE+¡ÏCFD=¡ÏEFD=90¡ã£¬
¡à¡÷EDFÊǵÈÑüÖ±œÇÈýœÇÐΣ®
µ±D¡¢E·Ö±ðΪAC¡¢BCÖеãʱ£¬ËıßÐÎCDFEÊÇÕý·œÐΣ®
¡ß¡÷ADF¡Õ¡÷CEF£¬
¡àS¡÷CEF=S¡÷ADF
¡àSËıßÐÎCEFD=S¡÷AFC£®
ÓÉÓÚ¡÷DEFÊǵÈÑüÖ±œÇÈýœÇÐΣ¬ÒòŽËµ±DE×îСʱ£¬DFÒ²×îС£»
ŒŽµ±DF¡ÍACʱ£¬DE×îС£¬ŽËʱDF=
BC=4£®
¡àDE=
DF=4
£»
µ±¡÷CEFÃæ»ý×îŽóʱ£¬ŽËʱ¡÷DEFµÄÃæ»ý×îС£®
ŽËʱS¡÷CEF=SËıßÐÎCEFD-S¡÷DEF=S¡÷AFC-S¡÷DEF=16-8=8£®
ÔòœáÂÛÕýÈ·µÄÊǢ٢ܢݣ®
¹ÊÑ¡D
 œâ£ºÁ¬œÓCF£»
œâ£ºÁ¬œÓCF£»¡ß¡÷ABCÊǵÈÑüÖ±œÇÈýœÇÐΣ¬
¡à¡ÏFCB=¡ÏA=45¡ã£¬CF=AF=FB£»
¡ßAD=CE£¬
¡à¡÷ADF¡Õ¡÷CEF£»
¡àEF=DF£¬¡ÏCFE=¡ÏAFD£»
¡ß¡ÏAFD+¡ÏCFD=90¡ã£¬
¡à¡ÏCFE+¡ÏCFD=¡ÏEFD=90¡ã£¬
¡à¡÷EDFÊǵÈÑüÖ±œÇÈýœÇÐΣ®
µ±D¡¢E·Ö±ðΪAC¡¢BCÖеãʱ£¬ËıßÐÎCDFEÊÇÕý·œÐΣ®
¡ß¡÷ADF¡Õ¡÷CEF£¬
¡àS¡÷CEF=S¡÷ADF
¡àSËıßÐÎCEFD=S¡÷AFC£®
ÓÉÓÚ¡÷DEFÊǵÈÑüÖ±œÇÈýœÇÐΣ¬ÒòŽËµ±DE×îСʱ£¬DFÒ²×îС£»
ŒŽµ±DF¡ÍACʱ£¬DE×îС£¬ŽËʱDF=
| 1 |
| 2 |
¡àDE=
| 2 |
| 2 |
µ±¡÷CEFÃæ»ý×îŽóʱ£¬ŽËʱ¡÷DEFµÄÃæ»ý×îС£®
ŽËʱS¡÷CEF=SËıßÐÎCEFD-S¡÷DEF=S¡÷AFC-S¡÷DEF=16-8=8£®
ÔòœáÂÛÕýÈ·µÄÊǢ٢ܢݣ®
¹ÊÑ¡D
µãÆÀ£ºŽËÌâ¿Œ²éÁËÈ«µÈÈýœÇÐεÄÅжšÓëÐÔÖÊ£¬ÒÔŒ°µÈÑüÖ±œÇÈýœÇÐεÄÅжšÓëÐÔÖÊ£¬ÊìÁ·ÕÆÎÕÈ«µÈÈýœÇÐεÄÅжšÓëÐÔÖÊÊǜⱟÌâµÄ¹ØŒü£®

Á·Ï°²áϵÁÐŽð°ž
Ïà¹ØÌâÄ¿
ÏÂÁÐŒÆËãÕýÈ·µÄÊÇ£š¡¡¡¡£©
A¡¢
| ||||||||||
B¡¢
| ||||||||||
C¡¢
| ||||||||||
D¡¢
|
2012Äê5ÔÂ8ÈÕ£¬¡°×îÃÀœÌÊŠ¡±ÕÅÀöÀòΪŸÈѧÉúÉힺÖØÉË£¬ÕÅÀÏÊŠÉጺŸÈÈ˵ÄÊÂŒ£ÊܵœÈ«¹úÈËÃñµÄŒ«Žó¹Ø×¢£¬ÔÚסԺÆڌ䣬¹²ÓÐ695ÍòÈËÒÔ²»Í¬·œÊœÏòËý±íÊŸÎʺòºÍ×£ž££¬œ«695ÍòÈËÓÿÆѧŒÇÊý·š±íʟΪ£š¡¡¡¡£©ÈË£®
| A¡¢6.95¡Á106 |
| B¡¢6.95¡Á105 |
| C¡¢69.5¡Á105 |
| D¡¢69.5¡Á106 |
ÏÂÁÐÔËËãÕýÈ·µÄÊÇ£š¡¡¡¡£©
A¡¢
| ||||
B¡¢£š
| ||||
| C¡¢£š-a2£©3=a6 | ||||
D¡¢a6¡Â£š
|
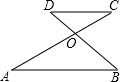 ÒÑÖª£¬ÈçÍŒ£¬ACÓëBDÏàœ»ÓÚµãO£¬AB¡ÎCD£¬Èç¹û¡ÏC=30.2¡ã£¬¡ÏB=50¡ã56¡ä£¬ÄÇÃŽ¡ÏBOCΪ£š¡¡¡¡£©
ÒÑÖª£¬ÈçÍŒ£¬ACÓëBDÏàœ»ÓÚµãO£¬AB¡ÎCD£¬Èç¹û¡ÏC=30.2¡ã£¬¡ÏB=50¡ã56¡ä£¬ÄÇÃŽ¡ÏBOCΪ£š¡¡¡¡£©| A¡¢80¡ã18¡ä |
| B¡¢50¡ã58¡ä |
| C¡¢30¡ã10¡ä |
| D¡¢81¡ã8¡ä |
 ÈçÍŒ£¬Ð¡Ã÷ÔÚŽóÂ¥30ÃמߣšŒŽPH=30Ã×£©µÄŽ°¿ÚPŽŠœøÐй۲⣬²âµÃÉœÆÂÉÏAŽŠµÄž©œÇΪ15¡ã£¬ÉœœÅBŽŠµÄž©œÇΪ60¡ã£¬ËÈÖªžÃɜƵÄƶÈi£šŒŽtan¡ÏABC£©Îª1£º
ÈçÍŒ£¬Ð¡Ã÷ÔÚŽóÂ¥30ÃמߣšŒŽPH=30Ã×£©µÄŽ°¿ÚPŽŠœøÐй۲⣬²âµÃÉœÆÂÉÏAŽŠµÄž©œÇΪ15¡ã£¬ÉœœÅBŽŠµÄž©œÇΪ60¡ã£¬ËÈÖªžÃɜƵÄƶÈi£šŒŽtan¡ÏABC£©Îª1£º