Question

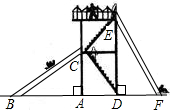如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，若∠CBA=32°，则∠FED=________度，∠EFD=________度．

Answer 1

32    58
分析：由两个长度相同的滑梯，所在的两个三角形△ABC，△DEF，又有AC=DF，∠BAC=∠EDF，就可以判断做两个三角形全等．利用互余关系求出另外一个角的度数．
解答：∵AC=DF，AB=DE，∠BAC=∠EDF=90°
∴Rt△ABC≌△DEF
∴∠FED=∠CBA=32°，∠EFD=90°-32°=58°．
故答案为：32，58．
点评：关键是根据两个长度相等，找他们所在的两个三角形全等；利用全等三角形的性质解题．解题的关键是证明△ABC≌△DEF，并利用全等的性质求解．