题目内容
6.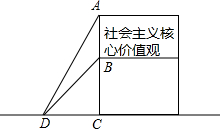 为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.
为了弘扬“社会主义核心价值观”,市政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°.(1)求公益广告牌的高度AB;
(2)求加固钢缆AD和BD的长.(注意:本题中的计算过程和结果均保留根号)
分析 (1)根据已知和tan∠ADC=$\frac{AC}{DC}$,求出AC,根据∠BDC=45°,求出BC,根据AB=AC-BC求出AB;
(2)根据cos∠ADC=$\frac{CD}{AD}$,求出AD,根据cos∠BDC=$\frac{CD}{BD}$,求出BD.
解答 解:(1)在Rt△ADC中,∵∠ADC=60°,CD=3,
∵tan∠ADC=$\frac{AC}{DC}$,
∴AC=3•tan60°=3$\sqrt{3}$,
在Rt△BDC中,∵∠BDC=45°,
∴BC=CD=3,
∴AB=AC-BC=(3$\sqrt{3}$-3)米.
(2)在Rt△ADC中,∵cos∠ADC=$\frac{CD}{AD}$,
∴AD=$\frac{3}{cos60°}$=$\frac{3}{\frac{1}{2}}$=6米,
在Rt△BDC中,∵cos∠BDC=$\frac{CD}{BD}$,
∴BD=$\frac{3}{cos45°}$=$\frac{3}{\frac{\sqrt{2}}{2}}$=3$\sqrt{2}$米.
点评 本题考查的是解直角三角形的知识,掌握仰角的概念和锐角三角函数的概念是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
16.估计$\sqrt{8}$-2的值在( )
| A. | 0到1之间 | B. | 1到2之间 | C. | 2到3之间 | D. | 3至4之间 |
17.已知四边形ABCD的四个顶点的坐标分别为A(-1,0),B(5,0),C(6,2),D(0,2),直线y=kx+2将该四边形分成面积相等的两部分,则k的值为( )
| A. | -$\frac{2}{5}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{4}{7}$ | D. | -$\frac{2}{7}$ |
14.不等式组$\left\{\begin{array}{l}{3(x+2)>2x+5}\\{\frac{x-1}{2}≤\frac{x}{3}}\end{array}\right.$的最小整数解是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
11.下列计算结果正确的是( )
| A. | a4•a2=a8 | B. | (a5)2=a7 | C. | (a-b)2=a2-b2 | D. | (ab)2=a2b2 |
15.下列命题中,属于真命题的是( )
| A. | 各边相等的多边形是正多边形 | |
| B. | 矩形的对角线互相垂直 | |
| C. | 三角形的中位线把三角形分成面积相等的两部分 | |
| D. | 对顶角相等 |
16.如果一组数据2,4,x,3,5的众数是4,那么该组数据的平均数是( )
| A. | 5.2 | B. | 4.6 | C. | 4 | D. | 3.6 |