题目内容
20.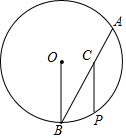 如图,⊙O中,弦AB=3,半径BO=$\sqrt{3}$,C是AB上一点且AC=1,点P是⊙O上一动点,连PC,则PC长的最小值是$\sqrt{3}$-1.
如图,⊙O中,弦AB=3,半径BO=$\sqrt{3}$,C是AB上一点且AC=1,点P是⊙O上一动点,连PC,则PC长的最小值是$\sqrt{3}$-1.
分析 过点O作OD⊥AB于点D,连接OP、OC,利用垂径定理和勾股定理可求出OC、OD的长度,然后利用三角形三边关系即可求出PC的最小值.
解答 解: 过点O作OD⊥AB于点D,连接OP、OC,
过点O作OD⊥AB于点D,连接OP、OC,
∵AB=3,
∴由垂径定理可知:BD=AD=$\frac{1}{2}$AB=$\frac{3}{2}$,
∵BO=$\sqrt{3}$,
∴由勾股定理可知:OD=$\frac{\sqrt{3}}{2}$,
∵AC=1,
∴CD=AD-AC=$\frac{1}{2}$,
∴由勾股定理可知:OC=1,
在△OCP中,由三角形三边关系可知:
PC>OP-OC,
∴当O、C、P三点共线时,PC可取得最小值,
此时PC=OP-OC=$\sqrt{3}$-1
故答案为:$\sqrt{3}$-1
点评 本题考查垂径定理,解题的关键是根据垂径定理和勾股定理求出OC的长度,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若直线x+3y+1=0与ax+y+1=0互相垂直,则实数a的值为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
12. 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
9.下列说法正确的是( )
| A. | 三角形的内心到三角形三个顶点的距离相等 | |
| B. | 三点确定一个圆 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 相等的弧所对的圆心角相等 |
10.关于抛物线y=-$\frac{1}{2}$(x+2)2+1,下列说法正确的是( )
| A. | 当x=2时,y有最小值1 | B. | 当x=-2时,y有最大值1 | ||
| C. | 当x=2时,y有最大值1 | D. | 当x=-2时,y有最小值1 |
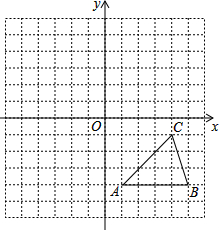 建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答.
建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答.