题目内容
求证：n边形的内角和等于（n-2）•180°．
已知：
求证：
证明： ．
已知：
求证：
证明：
考点：多边形内角与外角,三角形内角和定理
专题：证明题
分析：n边形的内角与外角和为180n°，外角和为360°，相减即为内角和．
解答：解：已知：一个多边形为n边形，
求证：它的内角和等于（n-2）•180°．
证明：∵n边形的内角与外角和为180n°，
又∵外角和为360°，
∴n边形的内角和等于180n°-360°=（n-2）•180°．
故答案为：一个多边形为n边形；它的内角和等于（n-2）•180°；
∵n边形的内角与外角和为180n°，
又∵外角和为360°，
∴n边形的内角和等于180n°-360°=（n-2）•180°．
求证：它的内角和等于（n-2）•180°．
证明：∵n边形的内角与外角和为180n°，
又∵外角和为360°，
∴n边形的内角和等于180n°-360°=（n-2）•180°．
故答案为：一个多边形为n边形；它的内角和等于（n-2）•180°；
∵n边形的内角与外角和为180n°，
又∵外角和为360°，
∴n边形的内角和等于180n°-360°=（n-2）•180°．
点评：本题考查了多边形的内角与外角．熟练记忆是关键．
练习册系列答案
相关题目
如图，点A、B、C三点均在⊙O上，∠B=∠C．以下结论错误的是（ ）| A、AB=AC | ||||
B、
| ||||
C、
| ||||
| D、∠BOC=80° |
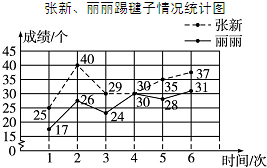体育老师要从每班选取一名同学，参加学校的秋季趣味运动会的踢毽子项目比赛．七年级二班张新和丽丽是踢毽子健将，下面是张新、丽丽几次踢毽子情况的统计图：
如图，已知∠AOC：∠BOC=1：3，∠AOD：∠BOD=5：7，若∠COD=15°，求∠AOB的度数．