题目内容
 如图,四边形ABCO是等腰梯形,OA∥BC且BC=CO,∠COA=60°,点O为平面直角坐标系的原点,点A的坐标为(4,0),B、C在第一象限,则直线AB的函数表达式为
如图,四边形ABCO是等腰梯形,OA∥BC且BC=CO,∠COA=60°,点O为平面直角坐标系的原点,点A的坐标为(4,0),B、C在第一象限,则直线AB的函数表达式为考点:等腰梯形的性质,待定系数法求一次函数解析式
专题:
分析:过B作BD⊥OA于D,利用等腰梯形的性质和已知条件可求B的坐标,设直线AB的函数表达式为y=kx+b,把A和B的坐标代入求出k和b的值即可.
解答:解: 过B作BD⊥OA于D,设OC=BC=x,
过B作BD⊥OA于D,设OC=BC=x,
∵四边形ABCO是等腰梯形,OA∥BC,∠COA=60°,
∴∠A=60°,
∵点A的坐标为(4,0),
∴OA=4,
∴AD=
,
∵∠DBA=30°,
∴AD=
AB=
x,
∴
=
x,
解得:x=2,
∴AD=1,BD=
,
∴B的坐标为(3,
),
∴直线AB的函数表达式为:y=-
x+4
,
故答案为:y=-
x+4
.
 过B作BD⊥OA于D,设OC=BC=x,
过B作BD⊥OA于D,设OC=BC=x,∵四边形ABCO是等腰梯形,OA∥BC,∠COA=60°,
∴∠A=60°,
∵点A的坐标为(4,0),
∴OA=4,
∴AD=
| 4-x |
| 2 |
∵∠DBA=30°,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 4-x |
| 2 |
| 1 |
| 2 |
解得:x=2,
∴AD=1,BD=
| 3 |
∴B的坐标为(3,
| 3 |
∴直线AB的函数表达式为:y=-
| 3 |
| 3 |
故答案为:y=-
| 3 |
| 3 |
点评:此题主要考查了一次函数的综合应用以及等腰梯形的性质和等腰三角形的性质等知识,题目的综合性较强,难度中等.

练习册系列答案
相关题目
已知甲乙两个立方体,甲的体积是乙的8倍,则甲的棱长是乙的( )
| A、8倍 | ||
| B、2倍 | ||
| C、521倍 | ||
D、
|
 如图,有许多个边长为a的小正方形、边长为b的大正方形以及长为b宽为a的长方形,取其中的若干个(三种图形都要取到)拼成一个长方形使其面积为(a+b)(a+2b),画出图形并根据图形回答(a+b)(a+2b)=
如图,有许多个边长为a的小正方形、边长为b的大正方形以及长为b宽为a的长方形,取其中的若干个(三种图形都要取到)拼成一个长方形使其面积为(a+b)(a+2b),画出图形并根据图形回答(a+b)(a+2b)=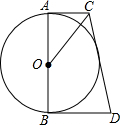 如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD,AC=2,BD=3,则AB的长是
如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD,AC=2,BD=3,则AB的长是