题目内容
已知|a-1|=4，|2-b|=5，求a-b的值．
考点：有理数的减法,绝对值
专题：
分析：根据绝对值的性质求出a、b，然后分情况讨论求解即可．
解答：
解：∵|a-1|=4，|2-b|=5，
∴a-1=±4，2-b=±5，
∴a=5或-3，b=7或-3，
当a=5，b=7时，a-b=5-7=-2，
a=-3，b=7时，a-b=-3-7=-10，
a=5，b=-3时，a-b=5-（-3）=8，
a=-3，b=-3时，a-b=-3-（-3）=0，
所以，a-b的值是-2或-10或8或0．
∴a-1=±4，2-b=±5，
∴a=5或-3，b=7或-3，
当a=5，b=7时，a-b=5-7=-2，
a=-3，b=7时，a-b=-3-7=-10，
a=5，b=-3时，a-b=5-（-3）=8，
a=-3，b=-3时，a-b=-3-（-3）=0，
所以，a-b的值是-2或-10或8或0．
点评：本题考查了有理数的减法，绝对值的性质，难点在于要分情况讨论．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
下列结论错误的是（ ）
| A、sin60°-sin30°=sin30° | ||
| B、sin30°=cos60° | ||
C、tan60°=
| ||
| D、sin245°+cos245°=1 |
如图，AB∥CD，直线EF与AB、CD相交于点E、F，若∠1=60°，则∠2的度数是下列运算中错误的有（ ）
①
=-3，②
=-5，③±
=3，④
=4．
①
| -32 |
| (-5)2 |
| 32 |
| 16 |
| A、4 | B、3 | C、2 | D、1 |
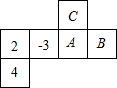如图是一个正方体的展开图，若正方体相对的面上的两个数互为相反数，则A，B，C三个数依次是（ ）| A、-2，-4，3 |
| B、3，-2，-4 |
| C、-2，3，-4 |
| D、3，-4，-2 |
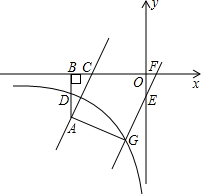如图，点A在反比例函数y=