题目内容
7.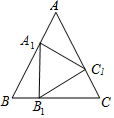 如图,等边三角形的边长为3,依次在AB、BC、AC上取点A1、B1、C1,使AA1=BB1=CC1=1,则△A1B1C1的面积是$\frac{3}{4}\sqrt{3}$.
如图,等边三角形的边长为3,依次在AB、BC、AC上取点A1、B1、C1,使AA1=BB1=CC1=1,则△A1B1C1的面积是$\frac{3}{4}\sqrt{3}$.
分析 过点A1作A1D∥BC,交AC于点D,构造出边长为1的小正三角形△AA1D;由AC1=2,AD=1,得点D为AC1中点,因此可求出S△AA1C1=2S△AA1D=$\frac{\sqrt{3}}{2}$;同理求出S△CC1B1=S△BB1A1=$\frac{\sqrt{3}}{2}$;最后由S△A1B1C1=S△ABC-S△AA1C1-S△CC1B1-S△BB1A1求得结果.
解答  解:如图所示,过点A1作A1D∥BC,交AC于点D,则∠AA1D=∠ADA1=60°,
解:如图所示,过点A1作A1D∥BC,交AC于点D,则∠AA1D=∠ADA1=60°,
∴△AA1D是边长为1的等边三角形.
又∵AC1=AC-CC1=3-1=2,AD=1,
∴点D为AC1的中点,
∴S△AA1C1=2S△AA1D=2×$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{2}$;
同理可得,S△CC1B1=S△BB1A1=$\frac{\sqrt{3}}{2}$,
∴S△A1B1C1=S△ABC-S△AA1C1-S△CC1B1-S△BB1A1=$\frac{\sqrt{3}}{4}$×32-3×$\frac{\sqrt{3}}{2}$=$\frac{3}{4}\sqrt{3}$.
故答案为:$\frac{3}{4}\sqrt{3}$.
点评 本题主要考查等边三角形的判定与性质,本题解题方法多种多样,解题时注意运用等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.

练习册系列答案
相关题目
17. 如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )
 如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )| A. | 北偏西30° | B. | 北偏西60° | C. | 东偏北30° | D. | 东偏北60° |
18.在平面直角坐标系中,已知点A(0,1),B(4,2),以原点O为位似中心,把△OAB按相似比1:2缩小,则点B的对应点B′的坐标是( )
| A. | (2,1) | B. | (-2,1) | C. | (2,1)或(-2,1) | D. | (2,1)或(-2,-1) |
15.下列长度的三条线段能组成三角形的是( )
| A. | 2,3,4 | B. | 3,3,6 | C. | 1,2,3 | D. | 5,10,4 |
2.对于数据:80,88,85,85,83,83,84.下列说法中错误的有( )
(1)这组数据的平均数是84; (2)这组数据的众数是85:
(3)这组数据的中位数是84;(4)这组数据的方差是36.
(1)这组数据的平均数是84; (2)这组数据的众数是85:
(3)这组数据的中位数是84;(4)这组数据的方差是36.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
12.下列调查中,最合适采用普查方式的是( )
| A. | 调查一批汽车的使用寿命 | |
| B. | 调查山东省市民春节期间计划外出旅游情况 | |
| C. | 调查某航班的旅客是否携带了违禁物品 | |
| D. | 调查全国初三学生的视力情况 |
16.若分式$\frac{3x-6}{2x+1}$的值为0,则x的值为( )
| A. | 2 | B. | 3 | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{2}$或2 |
17.对于函数y=-2x+4.下列说法错误的是( )
| A. | y随x的增大而减小 | B. | 它的图象与y轴的交点是(0,4) | ||
| C. | 当x<2时,y<0 | D. | 它的图象不经过第三象限 |