题目内容
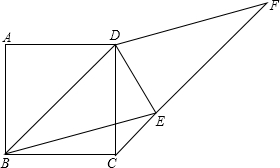 如图,正方形ABCD的边长为2,以对角线BD为边做菱形BEFD,点C、E、F在同一直线上,连接DE,有下列结论,①BE=2
如图,正方形ABCD的边长为2,以对角线BD为边做菱形BEFD,点C、E、F在同一直线上,连接DE,有下列结论,①BE=2| 2 |
考点:正方形的性质,菱形的性质
专题:
分析:由正方形ABCD可求出对角线BD的长,即可得出菱形的边BE的长,由平行线间的距离相等求出△BDE的高,即可求出S△BDE=2,在直角三角形中由边的关系求出∠DBE的度数,即可求出∠EBC,运用角的关键得出∠F=30°,∠BDF=150°,从而得出∠BDF=5∠F.
解答:解:∵正方形ABCD的边长为2,
∴BD=2
,
∵四边形BEFD是菱形,
∴BE=BD=2
.故①正确,
∵CF∥BD,AC⊥BD,
∴△BDE的高为AC的一半,即
,
∴S△BDE=
×2
×
=2,故②正确,
作EM⊥BD于点M,

∵ME=
,∠EMB=90°,BE=BD=2
,
∴∠MBE=30°,
∴∠EBC=45°-30°=15°,故③错误,
∵∠F=∠MBE=30°,
∴∠BDF=180°-30°=150°,
∴∠BDF=5∠F,故④正确.
∴结论正确的序号有①②④.
故答案为:①②④.
∴BD=2
| 2 |
∵四边形BEFD是菱形,
∴BE=BD=2
| 2 |
∵CF∥BD,AC⊥BD,
∴△BDE的高为AC的一半,即
| 2 |
∴S△BDE=
| 1 |
| 2 |
| 2 |
| 2 |
作EM⊥BD于点M,

∵ME=
| 2 |
| 2 |
∴∠MBE=30°,
∴∠EBC=45°-30°=15°,故③错误,
∵∠F=∠MBE=30°,
∴∠BDF=180°-30°=150°,
∴∠BDF=5∠F,故④正确.
∴结论正确的序号有①②④.
故答案为:①②④.
点评:本题主要考查了正方形的性质及菱形的性质,解题的关键是熟练的运用正方形的性质及菱形的性质求角及边的关系.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
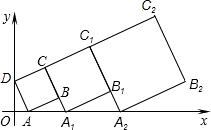 在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作第2个正方形A1B1ClC,延长C1B1交x轴于点A2:作第3个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为( )
在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作第2个正方形A1B1ClC,延长C1B1交x轴于点A2:作第3个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为( )A、5•(
| ||
B、5•(
| ||
C、5•(
| ||
D、5•(
|
 如图,在△ABC中,∠ACB=90°,AC=BC,点E在BC上,过点C作CF⊥AE于点F,延长CF使CD=AE,连接BD.求证:BD⊥BC.
如图,在△ABC中,∠ACB=90°,AC=BC,点E在BC上,过点C作CF⊥AE于点F,延长CF使CD=AE,连接BD.求证:BD⊥BC. 如图,在直角坐标系中,A(-4,-3),⊙A半径为1,P为x轴上的一动点,PQ切⊙A于点Q,则当PQ最短时,P点坐标是
如图,在直角坐标系中,A(-4,-3),⊙A半径为1,P为x轴上的一动点,PQ切⊙A于点Q,则当PQ最短时,P点坐标是 如图,已知直线AD、BE、CF相交于O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE=
如图,已知直线AD、BE、CF相交于O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE=