题目内容
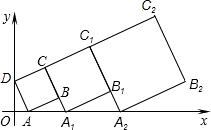 在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作第2个正方形A1B1ClC,延长C1B1交x轴于点A2:作第3个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为( )
在平面坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作第2个正方形A1B1ClC,延长C1B1交x轴于点A2:作第3个正方形A2B2C2C1,…按这样的规律进行下去,第2010个正方形的面积为( )A、5•(
| ||
B、5•(
| ||
C、5•(
| ||
D、5•(
|
考点:正方形的性质,坐标与图形性质
专题:规律型
分析:先由勾股定理就可以求出AD=
,第一个正方形的面积为5,由△A1BA∽△AOD就可以求出A1B=
,得出A1C=
,第二个正方形的面积为5×(
)2,再由△A2B1A1∽△AOD就可以求出A1B1=
,A2C1=(
)2
,第三个正方形的面积为:5×(
)4,根据规律可以得出第四个正方形的面积为5×(
)6,第五个正方形的面积为5×(
)8,…第n个正方形的面积为5×(
)2n-2.故可以得出第2010个正方形的面积.
| 5 |
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 4 |
| 3 |
| 2 |
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:∵四边形ABCD是正方形,
∴AD=AB=BC,∠DAB=90°.
∵A(1,0),D(0,2),
∴OA=1,OD=2.
在Rt△ADO中,由勾股定理,得
AD=
,
故第一个正方形的面积为5;
∵四边形A1B1ClC是正方形,
∴A1C=A1B1=B1C1,∠CA1B1=90°
∴△A1BA∽△AOD,
∴
=
,
∴A1B=
,
∴A1C=
,
∴第二个正方形的面积为5×(
)2;
∵△A2B1A1∽△AOD,
∴A1B1=
,
∴A2C1=(
)2
,
∴第三个正方形的面积为:5×(
)4;
根据规律可以得出
第四个正方形的面积为5×(
)6,
第五个正方形的面积为5×(
)8,
…
第n个正方形的面积为5×(
)2n-2.
当n=2010时,
第2010个正方形的面积为5×(
)4018.
故选D.
∴AD=AB=BC,∠DAB=90°.
∵A(1,0),D(0,2),
∴OA=1,OD=2.
在Rt△ADO中,由勾股定理,得
AD=
| 5 |
故第一个正方形的面积为5;
∵四边形A1B1ClC是正方形,
∴A1C=A1B1=B1C1,∠CA1B1=90°
∴△A1BA∽△AOD,
∴
| A1B |
| 1 |
| ||
| 2 |
∴A1B=
| ||
| 2 |
∴A1C=
3
| ||
| 2 |
∴第二个正方形的面积为5×(
| 3 |
| 2 |
∵△A2B1A1∽△AOD,
∴A1B1=
3
| ||
| 4 |
∴A2C1=(
| 3 |
| 2 |
| 5 |
∴第三个正方形的面积为:5×(
| 3 |
| 2 |
根据规律可以得出
第四个正方形的面积为5×(
| 3 |
| 2 |
第五个正方形的面积为5×(
| 3 |
| 2 |
…
第n个正方形的面积为5×(
| 3 |
| 2 |
当n=2010时,
第2010个正方形的面积为5×(
| 3 |
| 2 |
故选D.
点评:本题考查了点的坐标的运用,正方形的性质的运用,相似三角形的判定及性质的运用,正方形的面积公式的运用,规律的探究的运用,解答时探究出正方形的面积变化规律是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
在平面直角坐标系中,如果抛物线y=x2不动,而把x轴、y轴分别向上、向右平移1个单位,那么在新坐标系下抛物线的解析式是( )
| A、y=(x+1)2-1 |
| B、y=(x-1)2+1 |
| C、y=(x-1)2-1 |
| D、y=(x+1)2+1 |
 如图,AB∥CD,AC∥BD,下面推理不正确的是( )
如图,AB∥CD,AC∥BD,下面推理不正确的是( )| A、∵AB∥CD(已知)∴∠A=∠5(两直线平行,同位角相等) |
| B、∵AC∥BD(已知)∴∠3=∠4(两直线平行,內錯角相等) |
| C、∵AB∥CD(已知)∴∠1=∠2(两直线平行,內錯角相等) |
| D、∵AB∥CD(已知)∴∠3=∠4 (两直线平行,內錯角相等) |
化简
-
的结果是( )
| a2 |
| a-b |
| b2 |
| a-b |
| A、a+b |
| B、a-b |
| C、a2+b2 |
| D、1 |
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若y=kx-4的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1<y2,则k的值可能是下列的( )
| A、-4 | ||
B、-
| ||
| C、0 | ||
| D、1 |
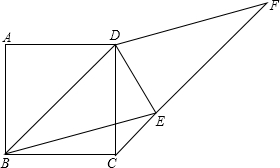 如图,正方形ABCD的边长为2,以对角线BD为边做菱形BEFD,点C、E、F在同一直线上,连接DE,有下列结论,①BE=
如图,正方形ABCD的边长为2,以对角线BD为边做菱形BEFD,点C、E、F在同一直线上,连接DE,有下列结论,①BE=