题目内容
6.已知二次函数y=2x2-mx-m2的图象与x轴有两个公共点A,B,且A点的坐标为(1,0),求B点坐标.分析 把已知点A的坐标代入可得m值,然后把m的值及y=0代入二次函数可求出点B的坐标.
解答 把(1,0)代入二次函数关系式,得0=2-m-m2,
∴m1=-2,m2=1,
当m=-2时,二次函数关系式为:y=2x2+2x-4,
令y=0,得:2x2+2x-4=0,
解得:x=1或-2,
∴二次函数图象与x轴有两个公共点的坐标是:(1,0),(-2,0);
又∵A点坐标为(1,0),则B(-2,0);
当m=1时,同理可得:B(-$\frac{1}{2}$,0).
综上可知:点B的坐标为(-2,0)或(-$\frac{1}{2}$,0).
点评 本题主要考查二次函数与方程的关系,掌握二次函数图象与x轴的交点横坐标为对应一元二次方程的两根是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
17.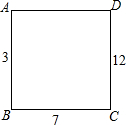 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )| A. | 2 | B. | 7 | C. | 8 | D. | 15 |
13.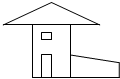 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
 如图所示的是一座房子的平面图,组成这幅图的几何图形有( )
如图所示的是一座房子的平面图,组成这幅图的几何图形有( )| A. | 三角形、长方形 | B. | 三角形、正方形、长方形 | ||
| C. | 三角形、正方形、长方形、梯形 | D. | 正方形、长方形、梯形 |
 自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:
自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看: