题目内容
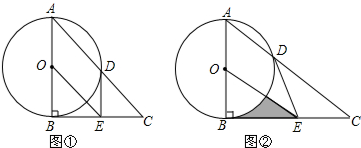
2．
如图，已知$\frac{AD}{DB}=\frac{AE}{EC}$，求证：△ADE∽△ABC．
分析 由比例的基本性质和已知条件可得：AD：AB=AE：AC，再根据两个三角形中，如果两组边对应成比例，且夹角相等，那么它们相似即可证明△ADE∽△ABC．
解答 证明：
∵$\frac{AD}{DB}=\frac{AE}{EC}$，
∴$\frac{AD}{AD+BD}=\frac{AE}{AE+CE}$，
∴$\frac{AD}{AB}=\frac{AE}{AC}$，
又∵∠A=∠A，
∴△ADE∽△ABC．
点评 本题考查相似三角形的判定，关键是知道两个三角形中，两组边对应成比例，且夹角相等的话，可互为相似三角形．
练习册系列答案
阅读快车系列答案
相关题目
10．下列说法正确的是（ ）
| A． | 正数和负数统称为有理数 | B． | 正整数包括自然数和零 | ||
| C． | 零是绝对值最小的整数 | D． | 非负数包括零和整数 |
17．两种移动电话计费方式表：
（1）一个月在本地通话200分和300分，按两种计费方式各需交多少线？
（2）对于某个本地通话时间，会出现两种计费方式的收费一样的情况吗？
（3）张老师想办一张电话卡，请你给他点建议．
| 全球通 | 神州行 | |
| 月租 | 50元/月 | 0 |
| 本地通话费 | 0.4元/分 | 0.6元/分 |
（2）对于某个本地通话时间，会出现两种计费方式的收费一样的情况吗？
（3）张老师想办一张电话卡，请你给他点建议．
