题目内容
14.在解方程组$\left\{\begin{array}{l}ax+3y=-2\\ 2x-by=7\end{array}\right.$时,由于粗心,甲看错了方程组中的a,而得解为$\left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$,乙看错了方程组中的b,而得解为$\left\{\begin{array}{l}x=5\\ y=1\end{array}\right.$,根据上面的信息解答:(1)甲把a看成了什么,乙把b看成了什么?
(2)求出原方程组的正确解.
分析 (1)把甲乙求得方程组的解分别代入原方程组即可;
(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.
解答 解:(1)把$\left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$代入方程组$\left\{\begin{array}{l}ax+3y=-2\\ 2x-by=7\end{array}\right.$得,$\left\{\begin{array}{l}{a=1}\\{b=5}\end{array}\right.$,
把$\left\{\begin{array}{l}x=5\\ y=1\end{array}\right.$代入方程组$\left\{\begin{array}{l}ax+3y=-2\\ 2x-by=7\end{array}\right.$得,$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$.
所以甲把a看成了1,乙把b看成了3.
(2)∵正确的a=-1,b=5,
∴$\left\{\begin{array}{l}-x+3y=-2\\ 2x-5y=7\end{array}\right.$,解得:$\left\{\begin{array}{l}x=11\\ y=3\end{array}\right.$.
点评 此题考查了二元一次方程组的解,解决本题的关键是明确方程组的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
相关题目
 如图,已知$\frac{AD}{DB}=\frac{AE}{EC}$,求证:△ADE∽△ABC.
如图,已知$\frac{AD}{DB}=\frac{AE}{EC}$,求证:△ADE∽△ABC. 如图,三角形A′B′C′是由三角形ABC沿射线AC方向平移2cm得到的,若AC=3cm,则A′C=1cm.
如图,三角形A′B′C′是由三角形ABC沿射线AC方向平移2cm得到的,若AC=3cm,则A′C=1cm.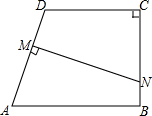 在四边形ABCD中,AB∥CD,∠C=90°
在四边形ABCD中,AB∥CD,∠C=90°