题目内容
【题目】四边形ADBC中，AC=BC，∠ACB=90°, ∠ADB=30°,AD=
,CD=14, 则BD=_________
【答案】
【解析】
作AH⊥BD于H，CN⊥BD于N，CM⊥HA于M，则四边形CMHN是矩形．首先证明△BCN≌△ACM，得四边形CMHN是正方形，设CN＝a．构建方程求出a即可解决问题；
解：作AH⊥BD于H，CN⊥BD于N，CM⊥HA于M，则四边形CMHN是矩形．
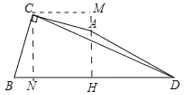
∵∠BCA＝∠MCN＝90°，
∴∠BCN＝∠MCA，
∵∠CNB＝∠M＝90°，BC＝CA，
∴△BCN≌△ACM，
∴CM＝CN，BN＝AM，
∴四边形CMHN是正方形，设CN＝a．
在Rt△AHD中，AD＝
，∠ADH＝30°，
∴AH＝
，DH＝
，
在Rt△CND中，∵CN2＋DN2＝CD2，
∴a2＋（a＋）2＝142，
解得a＝
或
（舍去），
∴AM＝BN＝
，
∴BD＝BN＋NH＋DH＝
，
故答案为：.
练习册系列答案
阅读快车系列答案
相关题目
