题目内容
13.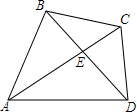 四边形ABCD中,对角线AC平分∠BAD,且满足∠BAD+∠BCD=180°,求证:$\frac{CB}{CE}$=$\frac{CA}{CB}$.
四边形ABCD中,对角线AC平分∠BAD,且满足∠BAD+∠BCD=180°,求证:$\frac{CB}{CE}$=$\frac{CA}{CB}$.
分析 根据∠BAD+∠BCD=180°,于是得到A,B,C,D四点共圆,根据圆周角定理得到∠CBD=∠CAD,由角平分线的定义得到∠BAC=∠CAD,等量代换得到∠BAC=∠CBE,证得△ABC∽△CBE,由相似三角形的性质即可得到结论.
解答 证明:∵∠BAD+∠BCD=180°,
∴A,B,C,D四点共圆,
∴∠CBD=∠CAD,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∴∠BAC=∠CBE,
∴∠BCE=∠ACB,
∴△ABC∽△CBE,
∴$\frac{CB}{CE}$=$\frac{CA}{CB}$.
点评 本题考查了相似三角形的判定和性质,四点共圆,圆周角定理,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
相关题目
1.若a、b互为相反数,c、d互为倒数,m的绝对值是2,则a+b+c×d+2×|m|=( )
| A. | 3 | B. | ±4 | C. | 5 | D. | 5或-3 |
3.一个正多边形的每个外角都等于36°,那么它是( )
| A. | 正五边形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
 已知函数y=-(x-m)2+n.
已知函数y=-(x-m)2+n.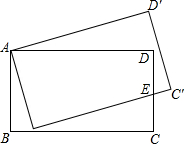 如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.
如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70. 如图,在?ABCD中,BE:EC=1:2,且S△BEF=2cm2,求S?ABCD.
如图,在?ABCD中,BE:EC=1:2,且S△BEF=2cm2,求S?ABCD.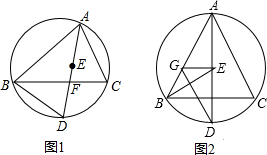
 如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.