题目内容
7．如图，A、C两点在直线L上，AC=6，D为射线CM上一点，CD=7，若在A、C两点之间栓一根橡皮筋，“奋力牛”Q拉动橡皮筋在平面内爬行，爬行过程中始终保持QA=2QC．（1）若Q点在直线L上，
①请在图中标出Q的位置；
②直接写出QC的长度，QC=2或6；
（2）在“奋力牛”爬行过程中，2QD+QA的最小值是14．
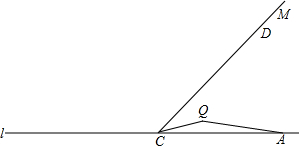
分析 （1）要分类讨论，当点Q在点C的左侧，当点Q在点C的右侧两种情况；
（2）因为QA=2QC，所以求2QD+QA的最小值就是求2QD+2QC的最小值．QD+QC≥CD，所以QD+QC最小值为CD=7，题中所求最小值为14．
解答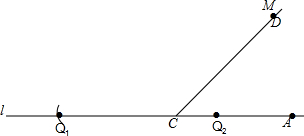 
解：（1）①如图所示：点Q即为所求；
②（Ⅰ）当点Q在点C的左侧，
∵QA=2QC，
∴CQ=AC=6，
（Ⅱ）当点Q在点C的右侧，
∵QA=2QC，
∴CQ=$\frac{1}{3}$AC=2．
故答案为：6或2；
（2）∵QA=2QC，
∴2QD+QA=2QD+2QC，
∵QD+QC≥CD，
∴QD+QC的最小值=CD=7，
∴2QD+QA的最小值=14．
故答案为；14．
点评 本题考查了基本作图，线段和的最小值，特别是（1）要进行分类讨论．
练习册系列答案
教材全解字词句篇系列答案
相关题目
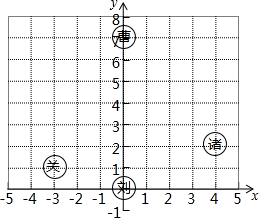三国时期的一次战役中，曹军的位置在（0，7），蜀军的3支部队位置如图所示，诸葛亮安排关羽先向北然后向东移动刘备向北移动，张飞先向北再向西移动，从三面围击曹军．
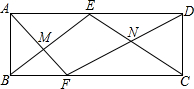如图，矩形ABCD中，点E、F分别在边AD、BC上，AF、BE交于M，DF、CE交于N，且△AME的面积是4，△BMF的面积是2，△DCN的面积是3．则矩形EMFN的面积是2$\sqrt{2}$+3．
12．已知$\left\{{\begin{array}{l}{x=-1}\\{y=2}\end{array}}\right.$是方程组$\left\{{\begin{array}{l}{ax+by+6=0}\\{bx-ay+7=0}\end{array}}\right.$的解，则a、b分别为（ ）
| A． | $\left\{{\begin{array}{l}{a=4}\\{b=1}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{a=-4}\\{b=-1}\end{array}}\right.$ | C． | $\left\{{\begin{array}{l}{a=-4}\\{b=1}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{a=4}\\{b=-1}\end{array}}\right.$ |
如图，?ABCD中，点O是AC与BD的交点，过点O的直线与BA、DC的延长线分别交于点E、F．