Question

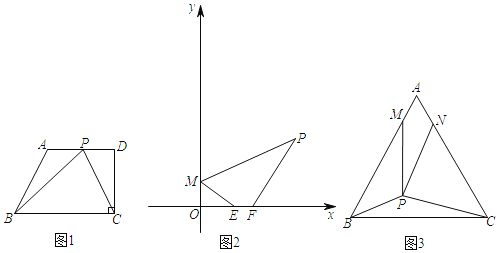
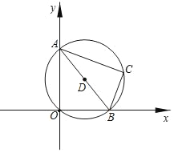
【题目】如图，在平面直角坐标系中，有一条长为10的线段AB，其端点A、点B分别在y轴、x轴上滑动，点C为以AB为直径的⊙D上一点（C始终在第一象限），且tan∠BAC=．则当点A从A0（0，10）滑动到O（0，0），B从O（0，0）滑动到B0（10，0）的过程中，点C运动的路径长为_____．

Answer 1

【答案】20﹣6．

【解析】

由∠AOB是直角,D为AB的中点,可得DO=5，由∠ACB=,AB=10,可得tan∠BAC=，可得tan∠AOC=tan∠ABC=2.可得点C在与y轴夹角为∠AOC的射线上运动，在计算出C运动的路径长即可.

解析:如图①,

连接OD∠AOB是直角,D为AB的中点,DO=5.

原点O始终在OD上,∠ACB=,AB=10,tan∠BAC=.BC=,AC=.

连接OC,则∠AOC=∠ABC, tan∠AOC=tan∠ABC=2. 点C在与y轴夹角为∠AOC的射线上运动.

如图②,

.

如图③,.

总路径长为+=20-,

故答案：20-.