题目内容
【题目】已知,点A(1,﹣![]() ),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
(1)求a的值与点B的坐标;
(2)将抛物线y=ax2(a≠0)平移,记平移后点A的对应点为A′,点B的对应点为B',若四边形ABB′A′为正方形,求平移后的抛物线的解析式.
【答案】(1)a=﹣![]() ,点B坐标(﹣2,﹣2).(2)y=﹣
,点B坐标(﹣2,﹣2).(2)y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 或y=﹣
或y=﹣![]() x2+
x2+![]() x﹣
x﹣![]() .
.
【解析】
(1)由点A、B在抛物线上,可得a的值与点B的坐标;
(2)由平移后点A的对应点为A′,点B的对应点为B',可得A′、B',利用四边形ABB′A′为正方形的性质求解即可.
解:(1)把点A(1,﹣![]() )代入y=ax2,得到a=﹣
)代入y=ax2,得到a=﹣![]() ,
,
∴抛物线为y=﹣![]() x2,
x2,
∴x=﹣2时,y=﹣2,
∴点B坐标(﹣2,﹣2),
∴a=﹣![]() ,点B坐标(﹣2,﹣2).
,点B坐标(﹣2,﹣2).
(2)∵四边形ABB′A′是正方形,
∴A′(﹣![]() ,
,![]() ),B′(﹣
),B′(﹣![]() ,1)或A′(
,1)或A′(![]() ,﹣
,﹣![]() ),B′(﹣
),B′(﹣![]() ,﹣5),
,﹣5),
设平移后的抛物线的解析式为y=﹣![]() x2+bx+c,
x2+bx+c,
则有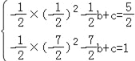 或
或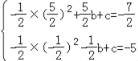 ,
,
解得![]() 或
或![]() ,
,
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 或y=﹣
或y=﹣![]() x2+
x2+![]() x﹣
x﹣![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目