��Ŀ����
����Ŀ������ͼ�α任���Գơ�ƽ�ƻ���ת��������и��⣺
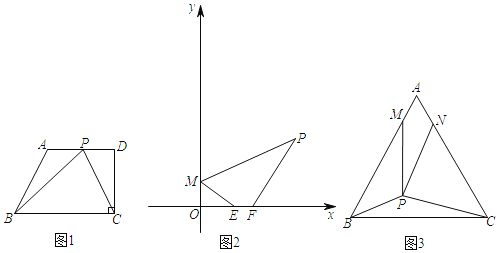
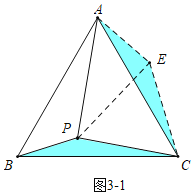
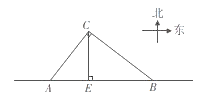
��1����ͼ1�����ı���ABCD�У�AD��BC��CD��BC����ABC��60����AD��8��BC��12����P�DZ�AD�ϵ�����һ�㣬����BPC�ܳ�����СֵΪ�� ��
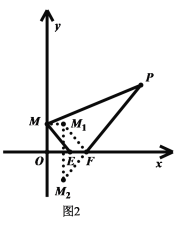
��2����ͼ2����֪M��0��1����P��2+![]() ��3����E��a��0����F��a+1��0������aΪ��ֵʱ���ı���PMEF���ܳ���С��
��3����E��a��0����F��a+1��0������aΪ��ֵʱ���ı���PMEF���ܳ���С��
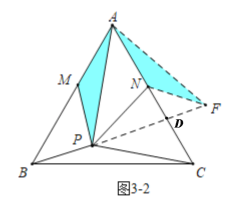
��3����ͼ3��PΪ�ȱ���ABC��һ�㣬��PB��2��PC��3����BPC��150����M��NΪ��AB��AC�ϵĶ��㣬��AM��AN����ֱ��д��PM+PN����Сֵ��
���𰸡���1��![]() ����2��a��
����2��a��![]() ʱ���ı���PMEF�ܳ���С����3��PM+PN����СֵΪ
ʱ���ı���PMEF�ܳ���С����3��PM+PN����СֵΪ![]() ��
��
��������
��1����ͼ1�������������ȸ�����ԳƵ����ʡ�����֮���߶���̵ó�![]() �ܳ���Сʱ����P��λ�ã��ٸ��ݾ��ε����ʡ�ֱ�������ε��������CD�ij����Ӷ��ɵ�
�ܳ���Сʱ����P��λ�ã��ٸ��ݾ��ε����ʡ�ֱ�������ε��������CD�ij����Ӷ��ɵ�![]() �ij���Ȼ�����ù��ɶ����ɵ�
�ij���Ȼ�����ù��ɶ����ɵ�![]() �ij����ɴ˼��ɵó��𰸣�
�ij����ɴ˼��ɵó��𰸣�
��2����ͼ2������������Ҫʹ�ı���PMEF���ܳ���С��ֻ��![]() ��С��������ƽ�ơ���ԳƵ����ʵó�
��С��������ƽ�ơ���ԳƵ����ʵó�![]() ���ٸ�������֮���߶���̵ó�
���ٸ�������֮���߶���̵ó�![]() ��Сʱ����F��λ�ã�Ȼ�����ô���ϵ�������ֱ��
��Сʱ����F��λ�ã�Ȼ�����ô���ϵ�������ֱ��![]() �Ľ���ʽ���Ӷ��ɵ�a��ֵ��
�Ľ���ʽ���Ӷ��ɵ�a��ֵ��
��3����ͼ�������������Ƚ�![]() �Ƶ�C˳ʱ����ת
�Ƶ�C˳ʱ����ת![]() ��������ת�����ʡ����ɶ������PA�ij����ٽ�
��������ת�����ʡ����ɶ������PA�ij����ٽ�![]() �Ƶ�A��ʱ����ת
�Ƶ�A��ʱ����ת![]() ��������ת�����ʡ�����֮���߶����ȷ��
��������ת�����ʡ�����֮���߶����ȷ��![]() ��Сʱ����N��λ�ã�Ȼ����ݵȱ������ε����ʼ��ɵó��𰸣�
��Сʱ����N��λ�ã�Ȼ����ݵȱ������ε����ʼ��ɵó��𰸣�
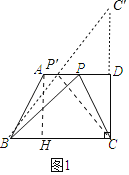
��1����ͼ1������C����ֱ��AD�ĶԳƵ�![]() ������
������![]() ��AD��
��AD��![]() ����
����![]()
����ԳƵ����ʡ�����֮���߶���̿�֪����ʱ![]() �ܳ���С����СֵΪ
�ܳ���С����СֵΪ![]()
��![]() ��H
��H
![]()
![]()
![]()
���ı���ADCH�Ǿ���
![]()
![]()
![]()
��![]() ��
�У�![]()
![]()
![]()
![]()
![]()
��![]() �ܳ�����СֵΪ
�ܳ�����СֵΪ![]()
�ʴ�Ϊ��![]() ��
��
��2���ı���PMEF���������У�PM��EF���ȹ̶�����ֻҪ![]() ��С���ı���PMEF���ܳ���ȡ����Сֵ
��С���ı���PMEF���ܳ���ȡ����Сֵ
��ͼ2������M����ƽ��1����λ���ȣ�EF�ij��ȣ�������![]()
��![]() ���ı���
���ı���![]() ��ƽ���ı���
��ƽ���ı���
![]()
����![]() ����x��ĶԳƵ�
����x��ĶԳƵ�![]() ������
������![]()
��![]() ��
��![]()
![]()
������֮���߶���̵ã�����![]() ����ʱ��
����ʱ��![]() ��С����СֵΪ
��С����СֵΪ![]()
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
����![]() �����
�����
���
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
����![]() �����
�����![]()
���![]()
�ʵ�![]() ʱ���ı���PMEF�ܳ���С��
ʱ���ı���PMEF�ܳ���С��
��3����ͼ3��1�У���![]() �Ƶ�C˳ʱ����ת
�Ƶ�C˳ʱ����ת![]() �õ�
�õ�![]() ������PE
������PE
����ת�����ʵã�![]()
![]() �ǵȱ�������
�ǵȱ�������
![]()
![]()
![]()
��ͼ3��2�У���![]() �Ƶ�A��ʱ����ת
�Ƶ�A��ʱ����ת![]() �õ�
�õ�![]() ������PF����AC�ڵ�D
������PF����AC�ڵ�D
����ת�����ʵã�![]()
![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]()
![]()
������֮���߶���̵ã�����N���D�غ�ʱ��![]() ��С����СֵΪPF
��С����СֵΪPF
��![]() ����СֵΪ
����СֵΪ![]() ��
��