题目内容
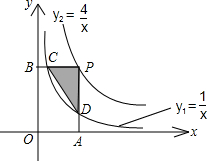
如图,已知双曲线 ,
, ,点P为双曲线
,点P为双曲线 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,则△PCD的面积为 .
于D、C两点,则△PCD的面积为 .
【答案】分析:根据BC×BO=1,BP×BO=4,得出BC= BP,再利用AO×AD=1,AO×AP=4,得出AD=
BP,再利用AO×AD=1,AO×AP=4,得出AD= AP,进而求出
AP,进而求出 PB×
PB× PA=CP×DP=
PA=CP×DP= ,即可得出答案.
,即可得出答案.
解答: 解:作CE⊥AO于E,DF⊥CE于F,
解:作CE⊥AO于E,DF⊥CE于F,
∵双曲线 ,
, ,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,
于D、C两点,
∴矩形BCEO的面积为:xy=1,
∵BC×BO=1,BP×BO=4,
∴BC= BP,
BP,
∵AO×AD=1,AO×AP=4,
∴AD= AP,
AP,
∵PA•PB=4,
∴ PB×
PB× PA=
PA= PA•PB=CP×DP=
PA•PB=CP×DP= ×4=
×4= ,
,
∴△PCD的面积为: .
.
故答案为: .
.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出 PB×
PB× PA=CP×DP=
PA=CP×DP= 是解决问题的关键.
是解决问题的关键.
 BP,再利用AO×AD=1,AO×AP=4,得出AD=
BP,再利用AO×AD=1,AO×AP=4,得出AD= AP,进而求出
AP,进而求出 PB×
PB× PA=CP×DP=
PA=CP×DP= ,即可得出答案.
,即可得出答案.解答:
 解:作CE⊥AO于E,DF⊥CE于F,
解:作CE⊥AO于E,DF⊥CE于F,∵双曲线
 ,
, ,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 于D、C两点,
于D、C两点,∴矩形BCEO的面积为:xy=1,
∵BC×BO=1,BP×BO=4,
∴BC=
 BP,
BP,∵AO×AD=1,AO×AP=4,
∴AD=
 AP,
AP,∵PA•PB=4,
∴
 PB×
PB× PA=
PA= PA•PB=CP×DP=
PA•PB=CP×DP= ×4=
×4= ,
,∴△PCD的面积为:
 .
.故答案为:
 .
.点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出
 PB×
PB× PA=CP×DP=
PA=CP×DP= 是解决问题的关键.
是解决问题的关键. 
练习册系列答案
相关题目
 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线