题目内容
1.①方程x2+5x-m=0的一个根是2,则m=14,另一个根是-7;②设a、b是方程x2+x-2010=0的两个实数根,则a2+2a+b的值为2009.
分析 ①根据方程x2+5x-m=0的一个根是2,将x=2代入原方程可得m的值,从而可以得到方程的另一个根;
②根据a、b是方程x2+x-2010=0的两个实数根,可得a2+a的值和a+b的值,从而可以得到a2+2a+b的值.
解答 解:①∵方程x2+5x-m=0的一个根是2,
∴22+5×2-m=0,
解得,m=14,
∴x2+5x-14=0,
解得,x1=-7,x2=2,
故答案为:14,-7;
②∵a、b是方程x2+x-2010=0的两个实数根,
∴a2+a-2010=0,a+b=$-\frac{1}{1}$=-1,
得a2+a=2010,
∴a2+2a+b=a2+a+a+b=2010+(-1)=2009,
故答案为:2009.
点评 本题考查一元二次方程的解和根与系数的关系,解题的关键是明确方程的根一定使得原方程成立和根与系数的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.据统计,怀柔雁栖湖常年总库容量38300000立方米,将38300000用科学记数法表示为( )
| A. | 0.383×108 | B. | 3.83×107 | C. | 38.3×106 | D. | 383×105 |

 表示一个正整数时,整数
表示一个正整数时,整数 可取的值是_______________________.
可取的值是_______________________.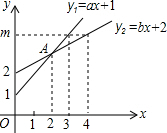 已知射线y1=ax+1与射线y2=bx+2在同一平面直角坐标系中的图象如图所示,则下列说法中①a=2b;②m=4;③点A的坐标为(2,3),正确的( )
已知射线y1=ax+1与射线y2=bx+2在同一平面直角坐标系中的图象如图所示,则下列说法中①a=2b;②m=4;③点A的坐标为(2,3),正确的( )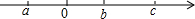 有理数a、b、c在数轴上的位置如图.
有理数a、b、c在数轴上的位置如图. 桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,不是其三视图的是( )
桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,不是其三视图的是( )


