题目内容
14. 在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=∠BOA=120°.
在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=∠BOA=120°.(1)以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′)(保留画图痕迹)
(2)求:①∠A′BC;②OA+OB+OC.
分析 (1)以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°即可得到△A′O′B.
(2)由旋转不变性可知:OA+OB+OC=CO+OO′+O′A′,所以只要证明C、O、O′、A′共线,则CA′=OA+OB+OC,在RT△BCA′中利用勾股定理即可求出CA′.
解答 解:(1)如图所示: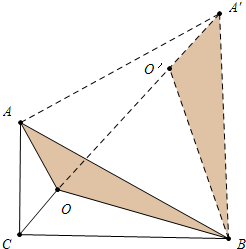
(2)∵△A′BO′是由△ABO顺时针旋转60°得到,
∴△OBO′,△ABA′是等边三角形,A′O′=AO
∴∠BOO′=∠BO′O=60°,OB=OO,∠ABA′=60°,
∵∠BOC=∠AOB=∠BO′A′=120°,
∴∠BOC+∠BOO′=180°,∠BO′O+∠AO′B=180°,
∴C、O、O′、A′共线,
∴AO+OB+OC=CO+OO′+A′O′=CA′,
在RT△ABC中,∵∠ABC=30°,AC=1,
∴AB=BA′=2,BC=$\sqrt{3}$,
∴∠CBA′=∠ABC+∠ABA′=90°,
∴CA′=$\sqrt{B{C}^{2}+BA{′}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$,
∴OA+OB+OC=$\sqrt{7}$.
点评 本题考查含有30度角的直角三角形的性质、等边三角形性质、旋转不变性、共线问题等知识,解题的关键是把不在同一直线上的三条线段转化为同一直线上的三条线段.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
| A. | y=(x+2)2+4 | B. | y=(x+2)2-4 | C. | y=(x-2)2+4 | D. | y=(x-2)2-4 |
5.已知扇形的圆心角为150°,半径为6cm,则该扇形的面积为( )
| A. | 5πcm2 | B. | 15πcm2 | C. | 20πcm2 | D. | 30πcm2 |
2.抛物线y=(x-3)2+1的对称轴是( )
| A. | 直线x=1 | B. | 直线x=3 | C. | 直线x=-1 | D. | 直线x=-3 |
9.抛三枚硬币,两个正面和一个反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{8}$ |
 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,$\sqrt{3}$)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.