题目内容
10．
如图，△ABC三边上的半圆面积从小到大依次记为S1，S2，S3，若S1+S2=S3，求证：△ABC是直角三角形．
分析 由S1+S2=S3，根据圆的面积公式得出$\frac{1}{8}$πAC2+$\frac{1}{8}$πBC2=$\frac{1}{8}$πAB2，即AC2+BC2=AB2，根据勾股定理的逆定理即可证明△ABC是直角三角形．
解答 证明：∵S1+S2=S3，S1=$\frac{1}{2}$π（$\frac{1}{2}$AC）2=$\frac{1}{8}$πAC2，同理S2=$\frac{1}{8}$πBC2，S3=$\frac{1}{8}$πAB2，
∴$\frac{1}{8}$πAC2+$\frac{1}{8}$πBC2=$\frac{1}{8}$πAB2，
即AC2+BC2=AB2，
∴△ABC是直角三角形．
点评 本题考查了勾股定理的逆定理和圆的面积的应用，关键是推出$\frac{1}{8}$πAC2+$\frac{1}{8}$πBC2=$\frac{1}{8}$πAB2，注意：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
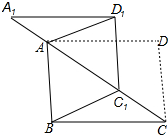如图，将?ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，分别连结AD、BC．
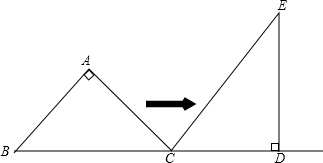等腰直角三角形△ABC的斜边BC与直角△CDE的直角边CD在同一直线上，∠A=∠EDC=90°，BC=DE=4，CE=5，将△ABC沿着BD向右平移，当点A落在CE上时，平移距离为$\frac{7}{2}$．
18．
与左边左视图所对应的实物图是（ ）
与左边左视图所对应的实物图是（ ）| A． |  | B． |  | C． |  | D． |  |
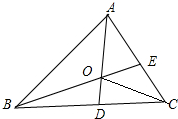如图，AD和BE是△ABC的角平分线且交于点O，连接OC，现有以下论断：