题目内容
16.⊙O的半径为R,圆心O到点A的距离为d,且R、d分别是方程x2-6x+9=0的两根,则点A与⊙O的位置关系是点A在⊙O上.分析 解方程得出R=d=3,即可得出点A在⊙O上.
解答 解:∵R、d分别是方程x2-6x+9=0的两根,
解方程得:R=d=3,
∴点A在⊙O上.
故答案为:点A在⊙O上.
点评 本题考查了点与圆的位置关系、一元二次方程的解法;熟练掌握点与圆的位置关系,通过解方程得出R=d=3是解决问题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
6.下列各式中,是最简二次根式的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{{a^2}+b}$ | D. | $\sqrt{{a^2}+2ab+{b^2}}$ |
7.下列去括号中,正确的是( )
| A. | a2-(1-2a)=a2-1-2a | B. | a2+(-1-2a)=a2-l+2a | ||
| C. | a-[5b-(2c-1)]=a-5b+2c-1 | D. | -(a+b)+(c-d)=-a-b-c+d |
6.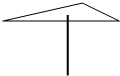 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )| A. | 三边高的交点 | B. | 三条角平分线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三边中线的交点 |
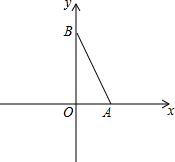 如图,在平面直角坐标系中,A(2,0),B(0,4).
如图,在平面直角坐标系中,A(2,0),B(0,4). 如图,已知AB=AC,∠ABE=∠ACD,BE与CD相交于O,求证:△ABE≌△ACD.
如图,已知AB=AC,∠ABE=∠ACD,BE与CD相交于O,求证:△ABE≌△ACD.