题目内容
 甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:(1)线段CD表示轿车在途中停留了
(2)线段DE对应的函数解析式为
(3)轿车从甲地出发后经过
考点:一次函数的应用
专题:图表型
分析:(1)根据函数的图象即可直接求解;
(2)利用待定系数法即可求解;
(3)求得直线OA和DE的解析式,求得交点坐标,即可求得轿车追上货车的事件;
求得BC的解析式,然后求OA和BC的交点坐标即可.
(2)利用待定系数法即可求解;
(3)求得直线OA和DE的解析式,求得交点坐标,即可求得轿车追上货车的事件;
求得BC的解析式,然后求OA和BC的交点坐标即可.
解答:解:(1)轿车在途中停留的时间是:2.5-2=0.5(小时),轿车比货车晚出发1小时,
故答案是:0.5,1;
(2)设线段DE的解析式是y=kx+b,
根据题意得:
,
解得:
,
则一次函数的解析式是:y=110x-195,
故答案是:y=110x-195;
(3)设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:
,
解得:
.
则轿车从甲地出发后经过3.9-1=2.9小时追上货车;
设BC的解析式是y=nx+c,
根据题意得:
,
解得:
,
则BC的解析式是:y=80x-80,
根据题意得:
,
解得:
,
则轿车在中途不停留并按原速度行驶,则货车出发后4h被轿车追上.
故答案是:2.9;4.
故答案是:0.5,1;
(2)设线段DE的解析式是y=kx+b,
根据题意得:
|
解得:
|
则一次函数的解析式是:y=110x-195,
故答案是:y=110x-195;
(3)设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:
|
解得:
|
则轿车从甲地出发后经过3.9-1=2.9小时追上货车;
设BC的解析式是y=nx+c,
根据题意得:
|
解得:
|
则BC的解析式是:y=80x-80,
根据题意得:
|
解得:
|
则轿车在中途不停留并按原速度行驶,则货车出发后4h被轿车追上.
故答案是:2.9;4.
点评:此题为一次函数的应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
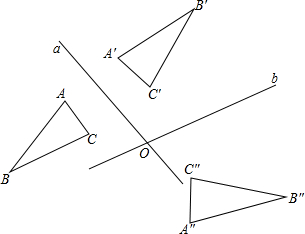 你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.
你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.