题目内容
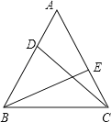
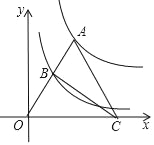
【题目】如图,点A为函数y=![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y=![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△OBC的面积为____.
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△OBC的面积为____.
【答案】6
【解析】
根据题意可以分别设出点A、点B的坐标,根据点O、A、B在同一条直线上可以得到A、B的坐标之间的关系,由AO=AC可知点C的横坐标是点A的横坐标的2倍,从而可以得到△OBC的面积.
设点A的坐标为(a,![]() ),点B的坐标为(b,
),点B的坐标为(b,![]() ),
),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a, ![]() )的直线的解析式为:y=kx,
)的直线的解析式为:y=kx,
∴![]() =ka,
=ka,
解得k=![]() ,
,
又∵点B(b, ![]() )在y=
)在y=![]() x上,
x上,
∴![]() =
=![]() b,解得,
b,解得,![]() =
=![]() 或
或![]() =
=![]() (舍去),
(舍去),
∴S△OBC=![]() =6.
=6.
故答案为:6.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目