题目内容
6.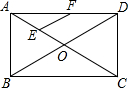 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6,∠BDA=30°,求EF的长度.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6,∠BDA=30°,求EF的长度.
分析 由矩形的性质和已知条件证出∠AOB=60°,证明△AOB是等边三角形,得出OA=OB=AB=6,OD=6,再证出EF是△AOD的中位线,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB=OD,
∴∠OAD=∠BDA=30°,
∴∠AOB=∠OAD+∠BDA=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=6,
∴OD=6,
∵点E、F分别是AO、AD的中点,
∴EF是△AOD的中位线,
∴EF=$\frac{1}{2}$OD=3.
点评 本题考查了矩形的性质、等边三角形的判定与性质、三角形中位线定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
11.下列多项式中不能用公式分解的是( )
| A. | -a2-b2+2ab | B. | a2+a+$\frac{1}{4}$ | C. | -a2+25b2 | D. | -4-b2 |
18.下面各图中,∠1与∠2是邻补角的是( )
| A. |  | B. |  | C. |  | D. |  |
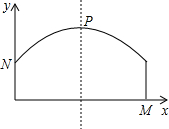 如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,某隧道横截面上的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成.矩形的长是12米,宽是3米,隧道的最大高度为6米,现以O点为原点,OM所在直线为x轴建立直角坐标系.