题目内容
17.在一个三角形中,若一条边等于另一条边的两倍,则称这种三角形为“倍边三角形”.(1)下列三角形是倍边三角形的是C
A.顶角为30°的等腰三角形
B.底角为30°的等腰三角形
C.有一个角为30°的直角三角形
D.有一个角为45°的直角三角形
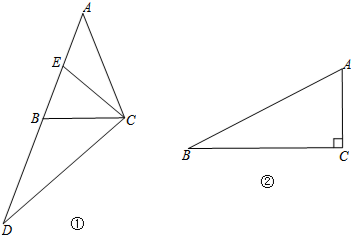
(2)如图①,在△ABC中,AB=AC,延长AB到D,使BD=AB,E是AB的中点.求证:△DCE是倍边三角形;
(3)如图②,Rt△ABC中,∠C=90°,AC=3,BC=6,若点D在边AB上(点D不与A、B重合),且△BCD是倍边三角形,求BD的长.
分析 (1)根据等腰三角形的性质和直角三角形的性质减小判断即可;
(2)根据两边对应成比例、夹角相等的两个三角形相似证明△ACD∽△AEC,再根据AD=2AC即可得到答案;
(3)分BC=2BD、BC=2CD、BD=2CD、CD=2BD四种情况进行解答,求出各种情况下BD的长.
解答 解:(1)顶角为30°的等腰三角形和底角为30°的等腰三角形的底与腰的关系无法确定,所以A、B不正确;
在直角三角形中,30°所对的直角边等于斜边的一半,∴C正确;
有一个角为45°的直角三角形斜边等于直角边的$\sqrt{2}$倍,D不正确,
故选:C;
(2)∵BD=AB=AC,∴AD=2AC.即$\frac{AD}{AC}$=2.
∵E是AB的中点,∴AB=2AE.∴AC=2AE.即$\frac{AC}{AE}$=2,
∴$\frac{AD}{AC}$=$\frac{AC}{AE}$.又∵∠A=∠A,
∴△ACD∽△AEC.∴$\frac{CD}{CE}$=$\frac{AD}{AC}$=2.
∴△DCE是倍边三角形.
(3)当BC=2BD时,BD=3;
当BC=2CD时,如图①,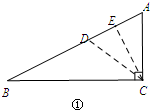
CD=3,作CE⊥AB于E,
tanA=$\frac{CE}{AE}$=$\frac{BC}{AC}$=2,
设AE=x,则CE=2x,AC=$\sqrt{5}$x,
∴$\sqrt{5}$x=3.x=$\frac{3}{5}$$\sqrt{5}$.
在△ACD中,∵CD=AC=3,CE⊥AB,
∴AD=2 AE=$\frac{6}{5}$$\sqrt{5}$.
∴BD=AB-AD=$\frac{9}{5}$$\sqrt{5}$;
当BD=2CD时,如图②,作DF⊥BC于F,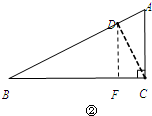 tanB=$\frac{DF}{BF}$=$\frac{AC}{BC}$=$\frac{1}{2}$,设DF=y,则BF=2y,BD=$\sqrt{5}$y,
tanB=$\frac{DF}{BF}$=$\frac{AC}{BC}$=$\frac{1}{2}$,设DF=y,则BF=2y,BD=$\sqrt{5}$y,
∴CD=$\frac{\sqrt{5}}{2}$y,CF=$\frac{1}{2}$y.
∵BC=BF+CF,∴6=2y+$\frac{1}{2}$y.
解得y=$\frac{12}{5}$.BD=$\frac{12}{5}$$\sqrt{5}$;
同理,当CD=2BD时,DF=$\frac{2\sqrt{19}-4}{5}$,BD=$\frac{2\sqrt{95}-4\sqrt{5}}{5}$.
综上所述,BD=3或$\frac{9}{5}$$\sqrt{5}$或$\frac{12}{5}$$\sqrt{5}$或$\frac{2\sqrt{95}-4\sqrt{5}}{5}$.
点评 本题考查的是相似三角形的判定和性质,理解新定义、正确运用三角形三角形的性质定理和判定定理是解题的关键,注意分情况讨论思想的运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 ,则A=( )
,则A=( ) B. 4
B. 4 C.
C. 
 (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣ (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形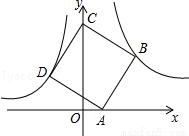
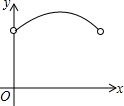
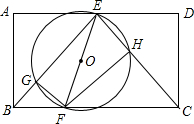 如图,矩形ABCD中,E为AD中点,点F为BC上的动点(不与B、C重合).连接EF,以EF为直径的圆分别交BE,CE于点G、H.设BF的长度为x,弦FG与FH的长度和为y,则下列图象中,能表示y与x之间的函数关系的图象大致是( )
如图,矩形ABCD中,E为AD中点,点F为BC上的动点(不与B、C重合).连接EF,以EF为直径的圆分别交BE,CE于点G、H.设BF的长度为x,弦FG与FH的长度和为y,则下列图象中,能表示y与x之间的函数关系的图象大致是( )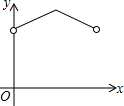
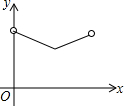
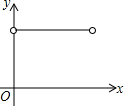
 早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直线)上学,途中发现忘带盒饭,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法: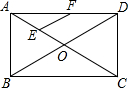 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6,∠BDA=30°,求EF的长度.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6,∠BDA=30°,求EF的长度.