题目内容
16.已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.先阅读下列解题过程:
解:因为a2c2-b2c2=a4-b4,①
所以c2(a2-b2)=(a2+b2)(a2-b2).②
所以c2=a2+b2.③
所以△ABC为直角三角形.④
问:(1)上述推理过程中,出现错误的两步是③④;
(2)本题的正确结论是△ABC是直角三角形或等腰三角形或等腰直角三角形.
分析 将等式右边的移项到方程左边,然后提取公因式将方程左边分解因式,根据两数相乘积为0,两因式中至少有一个数为0转化为两个等式;根据等腰三角形的判定,以及勾股定理的逆定理得出三角形为直角三角形或等腰三角形.
解答 解:∵a2c2-b2c2=a4-b4,
∴c2(a2-b2)=(a2+b2)(a2-b2),
移项得:c2(a2-b2)-(a2+b2)(a2-b2)=0,
因式分解得:(a2-b2)[c2-(a2+b2)]=0,
则当a2-b2=0时,a=b;当a2-b2≠0时,a2+b2=c2;
所以△ABC是直角三角形或等腰三角形或等腰直角三角形.
∴(1)上述推理过程中,出现错误的两步是③④;
(2)本题的正确结论是△ABC是直角三角形或等腰三角形或等腰直角三角形.
故答案为:③④,△ABC是直角三角形或等腰三角形或等腰直角三角形.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
7.下列坐标中,在直线y=x上的点的坐标是( )
| A. | (1,2013) | B. | (2013,1) | C. | (2013,2013) | D. | (-2013,2013) |
11.一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为( )
| A. | 6cm | B. | 12cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{6}$cm |
1.甲、乙两地相距100km,一辆汽车从甲地到乙地,则关于汽车到达乙地所用的时间t(h)与汽车的平均速度v(km/h)的函数图象说法正确的是( )
| A. | 图象在第一、三象限 | B. | 图象在第二、四象限 | ||
| C. | 图象在第一象限 | D. | 图象在第三象限 |
8.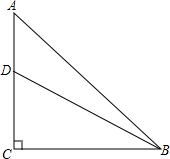 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
5.若线段a,b,c组成直角三角形,则它们的比为( )
| A. | 2:3:4 | B. | 3:4:6 | C. | 4:6:7 | D. | 7:24:25 |
6.两个相似三角形的对应边分别是15cm和25cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
| A. | 75cm,115cm | B. | 60cm,100cm | C. | 85cm,125cm | D. | 45cm,85cm |
 如图,OA,OB,OC,OD是⊙O的半径,
如图,OA,OB,OC,OD是⊙O的半径,