Question

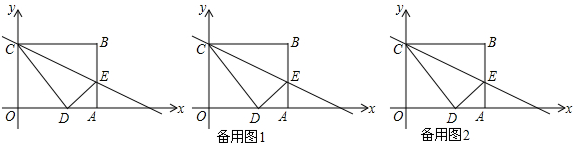
4．如图，平面直角坐标系中，矩形OABC，B（5，4），将矩形沿过点C的直线翻折，使点B落在线段OA上的点D处，折痕交AB于点E，P（m，0）是射线OA上一动点过点P作x轴的垂线，分别交直线CE和直线CB于点Q和点R．
（1）求点E的坐标；
（2）在点P的运动过程中，求$\frac{CR}{QR}$的值；
（3）设直线CE交x轴于点F，过点P作x轴的垂线交直线CD于点K，连接KE，当∠CKE=∠CFO时，求出m的值和线段CQ的长．

Answer 1

分析 （1）根据题意利用勾股定理得出DO的长，进而在Rt△DAE中，DE²=AD²+AE²，得出AE的值，即可得出答案；
（2）利用PQ∥AB，得出△CQR∽△CEB，进而求出答案；
（3）首先利用相似三角形的判定方法得出△KCE∽△FCD，进而利用待定系数法求出直线CD解析式以及直线CE解析式，即可表示出K点坐标，求出m的值，再利用勾股定理得出CQ的值．

解答 解：（1）设E（5，y），
∴AE=y，BE=4-y，
由题意可得：CD=BC=5，DE=BE=4-y，
在Rt△COD中，CO=4，
OD=$\sqrt{C{D}^{2}-C{O}^{2}}$=3，
∴AD=AO-DO=5-3=2，
在Rt△DAE中，DE²=AD²+AE²，
∴（4-y）²=2²+y²，
解得：y=$\frac{3}{2}$，
∴E（5，$\frac{3}{2}$）；

（2）如图1，

∵PQ⊥x轴，
∴PQ∥AB，
∴△CQR∽△CEB，
∴$\frac{CR}{QR}$=$\frac{CB}{EB}$=$\frac{5}{4-\frac{3}{2}}$=2；

（3）如图2，

∵∠CKE=∠CFO，∠KCE=∠FCD，
∴△KCE∽△FCD，
∴$\frac{CK}{CF}$=$\frac{CE}{CD}$，
∵C（0，4），E（5，$\frac{3}{2}$），
设直线CE解析式为y=kx+4，
∴$\frac{3}{2}$=5k+4，
解得：k=-$\frac{1}{2}$，
∴y=-$\frac{1}{2}$x+4，
∴F（8，0），
∴CF=$\sqrt{C{O}^{2}+F{O}^{2}}$=4$\sqrt{5}$，CE=$\sqrt{C{B}^{2}+B{E}^{2}}$=$\frac{5\sqrt{5}}{2}$，
∵C（0，4），D（3，0），
∴设直线CD解析式为y=k₁x+4，
∴0=3k₁+4，
∴k₁=-$\frac{4}{3}$，
∴y=-$\frac{4}{3}$x+4，
∴设K（m，-$\frac{4}{3}$m+4），
∴KR=|-$\frac{4}{3}$m+4-4|=$\frac{4}{3}$m，
∵CR=m，
∴CK=$\sqrt{C{R}^{2}+K{R}^{2}}$=$\sqrt{{m}^{2}+（\frac{4}{3}m）^{2}}$=$\frac{5}{3}$m，
∵$\frac{CK}{CF}$=$\frac{CE}{CD}$，
∴$\frac{\frac{5m}{3}}{4\sqrt{5}}$=$\frac{\frac{5\sqrt{5}}{2}}{5}$，
解得：m=6，
∵Q在直线CE上，
∴y=-$\frac{1}{2}$×6+4=1，
∴Q（6，1），
∴CQ=$\sqrt{C{R}^{2}+Q{R}^{2}}$=$\sqrt{{6}^{2}+（4-1）^{2}}$=3$\sqrt{5}$．

点评 此题主要考查了几何变换以及勾股定理、相似三角形的判定与性质、待定系数法求一次函数解析式等知识，根据题意画出正确图形，再结合相似三角形的性质求出m的值是解题关键．