题目内容
如图16①所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至长方形CE′F′ D′,旋转角为α.

图16
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图16②,G为BC中点,且0°<α<90°,求证:GD′= E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能,说明理由.
(1) 解:∵长方形CEFD绕点C顺时针旋转至长方形CE′F′ D′,
∴CD′=CD=2,在Rt△CED′中,CD′=2,CE=1,
∴∠CD′E=30°,∵CD∥EF,∴α=30°;
(2)证明:∵G为BC中点,∴CG=1,∴CG=CE,
∵长方形CEFD绕点C顺时针旋转至长方形CE′F′D′,
∴∠D′CE′=∠DCE=90°,CE=CE′.
∴∠GCD′=∠DCE′=90°+α.
在△GCD′和△E′CD中,
∴△GCD′≌△E′CD,∴GD′=E′D;
(3) 解:能.旋转角α为135°或315°

练习册系列答案
相关题目


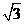 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第________秒.