题目内容
3.若自然数n使得作竖式加法n+(n+1)+(n+2)均不产生进位现象,则称n为“可连数”,例如32是“可连数”,因为32+33+34不产生进位现象;23不是“可连数”,因为23+24+25产生了进位现象,(1)那么小于10的“可连数”的个数为3; (2)那么小于200的“可连数”的个数为24.分析 解决此题首先要准确理解新的定义,然后根据新定义中“不产生进位”合理分析出各个数位上的值,列举即可.
解答 解:(1)由题意:若n为一位数,则有n+(n+1)+(n+2)<10,解得:n<3,所以:小于10的“可连数”有0、1、2,共3个.(2)由题意:小于200的“可连数”包含:一位数、两位数和百位数是1的三位数,由(1)知:满足条件的一位数有3个,两位数须满足:十位数可以是1、2、3,个位数可以是0、1、2,列举共有9个分别是10、11、12、20、21、22、30、31、32;三位数须满足:百位为1,十位数可以是0、1、2、3,个位数可以是0、1、2,列举共有12个,分别是:100、101、102、110、111、112、120、121、122、130、131、132所以:小于200的“可连数”有24个
点评 此题主要考察新定义的理解与分析,新定义中的“不产生进位”是分析的关键,即和不能大于10,在列举时要注意“不重不漏”.

练习册系列答案
相关题目
14.下列方程有实数根的是( )
| A. | x2-x+1=0 | B. | x2-1=0 | C. | x2-4x+5=0 | D. | x2-$\sqrt{2}$x+$\sqrt{3}$=0 |
11.若a2+am+9是一个完全平方式,那么m的值为( )
| A. | 6 | B. | -6 | C. | ±6 | D. | ±3 |
18.已知P1(a,-2)和P2(3,b)关于原点对称,则(a+b)2015的值为( )
| A. | 1 | B. | -1 | C. | -52015 | D. | 52015 |
15.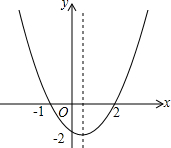 二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是( )
二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是( )
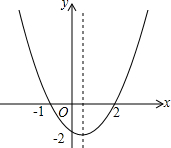 二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是( )
二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x=-1或x=2时,y=0 | D. | 当x>0时,y随x的增大而增大 |
12.在0,-13.48,5$\frac{1}{7}$,-$\frac{2}{3}$,-6,这些数中,负分数共有几个( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.下列等式中,成立的是( )
| A. | |+3|=±3 | B. | |-3|=-(-3) | C. | |±3|=±3 | D. | -|-3|=3 |