题目内容
15.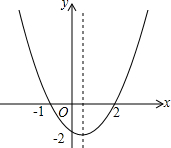 二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是( )
二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x=-1或x=2时,y=0 | D. | 当x>0时,y随x的增大而增大 |
分析 根据图象,判定开口方向以及函数的最值,找出与x轴的交点坐标,得出对称轴,结合图象得出增减性逐一解决问题.
解答 解:∵抛物线开口向上,
∴a>0,函数有最小值,所以A选项正确;
∵抛物线与x轴有2个交点为(-1,0),(2,0),
∴对称轴是直线x=$\frac{1}{2}$,所以B、C选项正确;
∵抛物线的对称轴为直线x=$\frac{1}{2}$,
∴当x>$\frac{1}{2}$时,y随x的增大而增大,所以D选项错误.
故选:D.
点评 此题考查二次函数的性质,二次函数图象与系数的关系,看清图象,找出与x轴的交点坐标,得出对称轴是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
20.下列计算正确的是( )
| A. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ | B. | $\sqrt{18}$=9$\sqrt{2}$ | C. | $\sqrt{27}$÷$\sqrt{3}$=3 | D. | $\sqrt{{2}^{2}}$=±2 |