题目内容
15.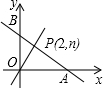 如图,一次函数y=-x+m的图象与x和y分别交于点A和点B,与正比例函数y=$\frac{3}{2}$x图象交于点P(2,n).
如图,一次函数y=-x+m的图象与x和y分别交于点A和点B,与正比例函数y=$\frac{3}{2}$x图象交于点P(2,n).(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在异与点P的另一点C,使得△OBC与△OBP的面积相等?若存在,请求出C点的坐标;若不存在,请说明理由.
分析 (1)将x=2代入正比例函数y=$\frac{3}{2}$x中即可求出n值,由此即可得出点P的坐标,将点P的坐标代入一次函数y=-x+m中即可求出m值;
(2)将x=0代入一次函数解析式中即可求出点B的值,再根据三角形的面积公式即可求出△POB的面积;
(3)根据△OBC与△OBP的面积相等即可求出点C的横坐标,将其代入正比例函数y=$\frac{3}{2}$x中即可求出点C的纵坐标,此题得解.
解答 解:(1)∵点P(2,n)在正比例函数y=$\frac{3}{2}$x图象上,
∴n=$\frac{3}{2}$×2=3,
∴点P的坐标为(2,3).
∵点P(2,3)在一次函数y=-x+m的图象上,
∴3=-2+m,解得:m=5,
∴一次函数解析式为y=-x+5.
∴m的值为5,n的值为3.
(2)当x=0时,y=-x+5=5,
∴点B的坐标为(0,5),
∴S△POB=$\frac{1}{2}$OB•xP=$\frac{1}{2}$×5×2=5.
(3)存在.
∵S△OBC$\frac{1}{2}$OB•|xC|=S△POB=5,
∴xC=-2或xC=2(舍去).
当x=-2时,y=$\frac{3}{2}$×(-2)=-3.
∴点C的坐标为(-2,-3).
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点P的横坐标利用正比例函数图象上点的坐标特征求出n值;(2)根据一次函数图象上点的坐标特征求出点B的坐标;(3)根据△OBC与△OBP的面积相等求出点C的横坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.1.996精确到0.01的近似数是( )
| A. | 2 | B. | 2.0 | C. | 1.99 | D. | 2.00 |
7.下列说法正确的是( )
| A. | 有理数分为正数和负数 | B. | 有理数的相反数一定比0小 | ||
| C. | 绝对值相等的两个数不一定相等 | D. | 有理数的绝对值一定比0大 |
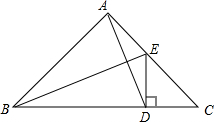 如图所示,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D,且BC=15,求AB+AE的长.
如图所示,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D,且BC=15,求AB+AE的长. 如图,直线AB,CD相交于点O,∠BOE=90°,OF平分∠AOD,∠COE=20°,求∠BOD与∠DOF的度数.
如图,直线AB,CD相交于点O,∠BOE=90°,OF平分∠AOD,∠COE=20°,求∠BOD与∠DOF的度数.